| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 2023공공빅데이터청년인재양성후기
- 2023공공빅데이터청년인재양성
- ML
- data
- decisiontree
- machinelearning
- k-means
- 머신러닝
- textmining
- 공빅
- DL
- NLP
- 공빅데
- 공공빅데이터청년인재양성
- Keras
- 텍스트마이닝
- 데이터전처리
- ADsP3과목
- datascience
- ADSP
- 빅데이터
- 2023공빅데
- 분석변수처리
- 데이터분석
- Kaggle
- DeepLearning
- 클러스터링
- SQL
- 오버샘플링
- 공공빅데이터청년인턴
- Today
- Total
愛林
Python으로 배우는 데이터 전처리 이해(II) - 분석변수 처리 - 차원 축소(Dimensionality Reduction) 본문
Python으로 배우는 데이터 전처리 이해(II) - 분석변수 처리 - 차원 축소(Dimensionality Reduction)
愛林 2022. 7. 13. 23:23
드디어 전처리가.. 끝나간다...!

Intro
전처리에 대해 배우고 있다.
전처리란 데이터에서 중요한 요소를 뽑아내고, 데이터의 다양성과 데이터 형태의 품질을 확보하는 것이다.
데이터 전처리 과정에는 데이터 정제와 분석변수처리가 있는데,
우리는 분석변수처리에 대해 공부하고 있다.
분석변수처리에는 데이터 축소, 파생변수 생성, 데이터 변환, 불균형 데이터 처리가 있다.
이전 시간에는 불균형 데이터를 처리하는 법에 대하여 알아보았다.불균형 데이터를 처리하는 방법에는 오버샘플링과, 언더샘플링이 있었다.
직전에는 오버샘플링(OverSampling) 을 진행했다.오버 샘플링은 낮은 클래스의 데이터를 높은 클래스의 데이터 양만큼 데이터 수를 늘려서비율을 맞추어 주는 것이다.
https://wndofla123.tistory.com/31
Python으로 배우는 데이터 전처리 이해(II) - 불균형 데이터 처리(Imbalanced Data) - 오버 샘플링(Over Sam
Intro 이전 게시물 https://wndofla123.tistory.com/30 공공빅데이터 청년인턴/데이터Python으로 배우는 데이터 전처리 이해(II) - 불균형 데이터 처리(Imb Intro 데이터 전처리 과정에서 분석 변수 처리 과정에..
wndofla123.tistory.com
여기에.. 말은 하지 않았으나(그냥 놓친 거다 ㅠ)
분석 변수 처리에 추가되는 것이 있었으니 ..
바로.. 차원축소이다.
오늘은 드디어 데이터 전처리의 마지막 .. 차원 축소에 대해 알아보자.
차원의 저주 (Curse of dimensionality)
차원의 저주란, 확보하고 있는 데이터의 양을 포함하는 차원이 증가 할수록, 필요 데이터의 부족으로 인하여
과적합 등의 문제로 다른 문제들이 발생하여 모델의 성능이 저하되는 현상이다.
(필요 데이터가 품귀해지는 현상)
- > 변수가 증가할수록 우리는 모델을 충분하게 학습시키는 것이 어려워진다.
다중공선성 (Multicollinearity)
다중회귀분석에서 독립변수들 간의 상관관계가 나타나는 문제이다.
독립변수는 독립변수니까 상관관계가 있어서는 안 된다. (종속변수면 몰라)
예를 들어 성별 변수와 주민번호 뒷자리의 첫번째 수가 성별을 의미하는 것처럼, 같은 의미를 가지고 있는
변수가 두 개일 경우, 강한 상관관계를 나타내게 된다.
이는 곧 편향을 발생시킬 수있다는 말이 된다.
그래서 중복된 값이 들어있는 변수는 제거가 필요하다.
차원 축소 (Dimensionality Reduction)
분석 효율성(분석 과정의 비용 최적화) 과 효과성(결과의 정확성)을 위해서는 비즈니스의 의미와 특성을 보존하면서
변수를 줄이는 과정이 필요하다. 이것이 바로 차원축소.
차원 축소의 유형에는 특성 추출과 특성 선택이 있다.
■ 특성 추출(Feature Extraction)
여러 변수들 간의 관계를 파악하여 이를 대표하는 선형 혹은 비선형 결합을 활용해 새로운 특성을 추출하는 기법
여러 변수들의 의미를 포함하는 특성을 추출하여 줄이는 기법이다.
■ 특성 선택 (Feature Selection) = 변수 선택
여러 변수들 중 주요 특성을 가지는 변수만 선택하는 기법이다.
변수 선택의 필터 기법, 래퍼 기법, 임베디드 기법 등이 있다.
차원 축소 기법
차원 축소 알고리즘을 사용하기 위해서는 각 분석 변수들 간의 독립성 확인이 필요하다.
■ 주성분 분석 (Principal Component Analysis, PCA)
고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간으로 변환하는 기법.
여러 변수들의 선형결합으로 이루어진 새로운 변수 주성분을 만들어 기존 변수들이
가지고 있는 의미를 포함해서 차원을 축소한다.
고차원 데이터 집합이 주어졌을 때 원래의 고차원 데이터와 가장 비슷하면서 더 낮은 차원 데이터를 찾아내는 방법

■ 요인 분석( Factor Analysis, FA )
데이터에 관찰할 수 있는 잠재적 변수가 존재한다고 가정하여, 모형을 세운 뒤 관찰 가능한
데이터를 이용하여 해당 잠재요인을 도출하고 데이터 구조를 해석하는 기법 (FCA포함)
공분산 정방형 행렬을 사용한다.
다수 변수들을 변수들 간의 상관관계 분석을 하여 공통 차원들을 통해 축약하는 통계 기법이다.
전체를 하나로 축약.
■ 특이값 분해 (Singular Value Decomposition, SVD)
선형 대수의 일반적 기법이며, 실수 공간에 정의된 M x N 차원의 행렬 데이터에서
특이값을 추출하고 이를 통해 주어진 데이터 세트를 효과적으로 축약할 수 있는 기법이다.
■ 다차원 척도법 (Multi imensional Scaling, MDS)
개체들 사이의 유사성, 비유사성을 측정하여 2차원 또는 3차원 공간상에
점으로 표현하여 개체들 사이의 집단화를 시각적으로 표현하는 분석 방법이다.

■ 판별 분석 (Discriminant Analysis)
집단을 구분할 수 있는 설명변수를 통하여 집단 구분하는 기법이다.
소속된 집단을 예측하는 목적과 함수식을 도출하는 통계 기법.
■ t-SNE (t-distributed stochastic neighbor embedding)
고차원 데이터를 2차원 또는 3차원의 저차원 데이터로 시각화하여 데이터
분석 과정에서 활용하기 위한 방법이다.
데이터 간 거리를 통계적 확률로 변환하여 임베딩에 이용하기 때문에 안정적인 임베딩 학습 결과를 나타낸다.
차원 분석 실습
■ PCA
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
import os
if os.name =='nt' :
font_family = "Malgun Gothic"
else :
font_family = "AppleGothic"
# 값이 깨지는 문제 해결을 위해 파라미터값 설정
sns.set(font=font_family, rc = {"axes.unicode_minus" : False})
먼저 필요한 라이브러리들을 import 해준다.
우리는 붓꽃 데이터를 이용하여 실습을 진행할 것이므로 , 붓꽃 데이터를 로드해준다.
from sklearn.datasets import load_iris
iris = load_iris()

붓꽃 데이터의 특성은 이러하다.
데이터 프레임을 생성해주고 실습을 준비하자.

데이터 프레임에 target 이라는 변수를 새로 생성해주었다.
target 은 iris 의 종류를 알려주는 데이터이다.
참고로, 0은 'setosa', 1은 'versicolor', 2는 'virginica'를 의미한다 .
(iris['target_names]로 확인 가능)
이제 이 붓꽃 데이터를 시각화해보자.
# 시각화
# setosa 는 세모, versicolor는 네모, virginica 는 동그라미로 표현
markers = ['^', 's', 'o']
# setosa 는 target 값은 0, versicolor는 1, virginica는 2.
# 각 target별로 다른 shape으로 scatter plot
setosa 는 ^ (target 값 0)
, versicolor 는 s(네모, target 값 1)
, virginica 는 o(target 값 2)
로 표현한다.
이 데이터를 산점도로 표현해보자.

sepal 은 꽃잎을 말하고,
petal 은 꽃받침을 말한다.
시각화를 끝냈으니, 이제 주성분 분석(PCA) 를 해보자.
주성분 분석은 여러 변수들의 선형결합으로 이루어진 새로운 변수 주성분을 만들어 기존 변수들이
가지고 있는 의미를 포함해 차원을 축소 하는 기법이었다.
개별속성을 함께 스케일링하고,
PCA 로 압축하기 전에 각 속성값을 동일한 스케일로 변환하는 것이 필요하다.
from sklearn.preprocessing import StandardScaler # PCA 전 특성에 대한 스케일링
iris_scaled = StandardScaler().fit_transform(df.iloc[:, :-1])
iloc[] 은 이전에 우리가 pandas 기초를 공부할 때, 위치를 기반으로 하는 인덱스라고 배웠다.

이제 pca 변환된 데이터의 컬럼명을 명명하고, irisDF_pca 데이터프레임을 만들어준다.
PCA는 2차원 데이터 집합에 대해 PCA를 수행하면 2개의 서로 수직인 주성분 벡터를 반환해준다.
그래서 150개의 데이터가 2개의 주성분 벡터로 표현된다.
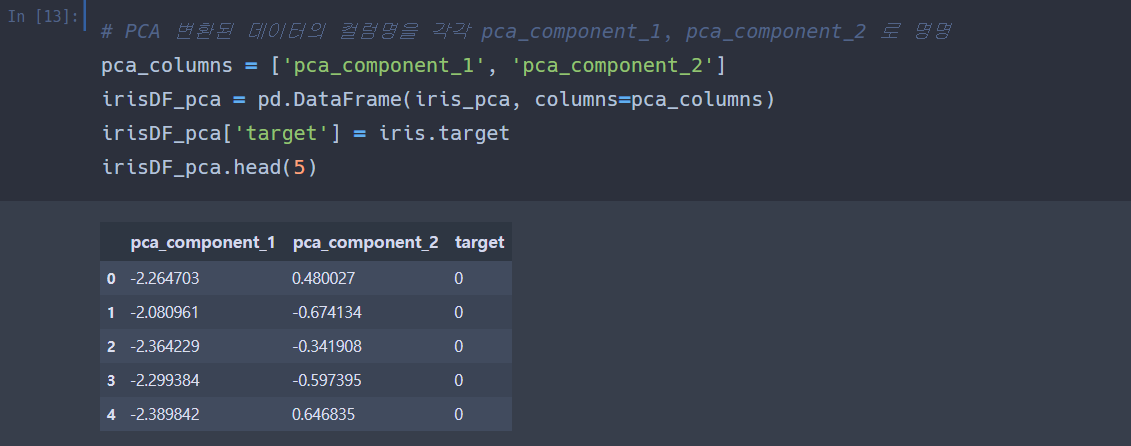
이제 원본 데이터와 PCA데이터로 분류 모델을 실행한다.
랜덤 포레스트 알고리즘으로 교차 검증을 수행한다.
교차검증이란, 과적합을 막기 위해 훈련 데이터 세트를 바꾸어가면서 나온 정확도를
평균하여 보는 것이다.
rcf = RandomForestClassifier(random_state= 156)
scores = cross_val_score(rcf, iris.data, iris.target, scoring = 'accuracy', cv= 3)
# cross_val_score 가 교차검증을 수행해주는 것위는 원본 데이터.
cross_val_score 는 교차검증을 더 수월하게 해주는 API 이다.
rct 는 랜덤포레스트 알고리즘, iris.data , iris.target 이 label ,
scoring 은 뭐가 많은데 암튼 정확하게. accuracy 로 ^^.. 예측 성능 평가 데이터 지표라고 한다.
cv 는 교차 검증 폴드 수이다. 우리는 3개의 폴드를 검증할 것이니 3개.

원본 데이터의 교차 검증 수행결과이다.

PCA 한 것을 넣어주고, 랜덤포레스트 알고리즘을 시행하고,
암튼 위에서 했던 거 똑같이 해준다.
우리가 PCA 해준 것의 교차 검증 수행결과가 나왔다.
근데 이거 원래 교차 검증 정확도가 낮아지나 ? 다중공선성이 낮아진 것이라고 볼 수 있을까..?
누가 좀 알려줘
■ t-SNE
t-SNE 방법은 고차원 데이터를 2차원 또는 3차원의 저차원 데이터로 시각화하여 데이터
분석 과정에서 활용하기 위한 방법이다. 아무튼 차원을 낮추어서 간단하게 보여준다는 뜻인듯.


target 정보를 2차원으로 같이 눌러주어서는 안되므로,
일단 target 정보를 지운 train_df 데이터프레임을 다시 만들어주었다.
이제 이걸 2차원 t-SNE 임베딩 해보자.
2차원으로 꾹꾹 눌러보는거다.

2차원으로 꾹꾹 눌러담은 우리의 붓꽃데이터들이다.
이제 다시 target 정보를 불러온다.

#target별 분리
tsne_df_0 = tsne_df[tsne_df['target'] == 0]
tsne_df_1 = tsne_df[tsne_df['target'] == 1]
tsne_df_2 = tsne_df[tsne_df['target'] == 2]
# target 별 시각화
plt.scatter(tsne_df_0['component 0'], tsne_df_0['component 1'], color = 'blue', label = 'setosa')
plt.scatter(tsne_df_1['component 0'], tsne_df_1['component 1'], color = 'red', label = 'versicolor')
plt.scatter(tsne_df_2['component 0'], tsne_df_2['component 1'], color = 'green', label = 'virginica')
plt.xlabel('component 0')
plt.ylabel('component 1')
plt.legend()
plt.show()
냅다 시각화 !

강의안에 있는거랑 조금 .. 다른데 ..? 아무튼 비슷하게 나왔다 ;
근데 거울모드를 해버린 ..
Review
이번엔 데이터 전처리 안에서 분석 변수 처리의 마지막, 차원축소를 했다.
차원 축소란,
분석 효율성(분석 과정의 비용 최적화) 과 효과성(결과의 정확성)을 위해서 여러 개의 변수를
축소하여 적은 수의 변수로 압축(?) 시켜주는 방법이다.
차원 축소 기법에는 t-SNE, PCA 말고도 많지만,
우리는 이 두 가지를 실습했다.
PCA 기법은 주성분 분석이라는 기법인데,
거창하게 말할 것 없이 그냥 여러 변수들의 정보를 압축한 주성분을 만들어 차원을 축소하는 것이다.
우리는 2차원 벡터로 축소시켰다.
t-SNE 기법은 고차원 데이터를 저차원으로 낮추어 주는 기법인 것은 같으나,
직접적으로 차원을 축소시킨다기보다는,
고차원 데이터를 낮은 차원의 눈으로 볼 수 있게(?) 아무튼 간에 시각화해주는 것이다.
드디어 전처리가 끝났다.
전처리 대전 끝!!!
이제 웹크롤링 스크래핑... 통계 기반 데이터 분석 하자...




