| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 공빅
- k-means
- 2023공빅데
- data
- 2023공공빅데이터청년인재양성
- datascience
- 클러스터링
- 공빅데
- 빅데이터
- 오버샘플링
- 데이터분석
- Keras
- 데이터전처리
- machinelearning
- 공공빅데이터청년인턴
- 공공빅데이터청년인재양성
- 텍스트마이닝
- ADSP
- ML
- ADsP3과목
- 2023공공빅데이터청년인재양성후기
- 머신러닝
- textmining
- Kaggle
- DL
- decisiontree
- 분석변수처리
- DeepLearning
- NLP
- SQL
- Today
- Total
愛林
[Python/Statistics] 기초통계실습 - 기술 통계(Descriptive Statistics) 본문
기술통계 (Descriptive Statistics)
평균, 분산, 표준편차 등에 대해 알아보는 시간이었다.
기술통계 (Descriptive statistics) 는,
조사 및 측정된 자료를 통해 그 자료가 가지고 있는 특징을 수치, 표, 그래프로 정리하는 과정이다.
기술 통계 기법으로는
평균값, 중앙값, 최빈값, 최대값, 최소값, 범위, 분산, 표준편차, 그래프 등이 있다.
탐색적 데이터 분석이라고 하기도 한다. - > 기술통계이다.
● 탐색적 데이터 분석의 주제는 4가지가 있는데,
1. 저항성의 강조
저항성이란, 데이터의 일부가파손되었을 때 영향을 적게 받는 성질을 말한다.
2. 잔차의 해석
잔차란, 관찰값들이 주경향으로부터 얼마나 벗어나는 지를 알 수 있는 척도이다.
3. 데이터의 재표현
데이터의 해석과 분석을 단순화하기 위해 원 변수를 재표현하는 방법이다.
로그 변환 등으로 왜도가 큰 그래프를 좌우대칭으로 만들어주는 방법 등이 있다.
4,데이터의 현시성
데이터를 그래프로 시각화함으로서 데이터 안에 숨겨진 정보를 효율적으로 파악한다.
기술통계 실습
import pandas as pd
import numpy as np
오늘도 필요한 라이브러리는 import 해주고 간다.
data = pd.DataFrame (
{ "score1" : [99, 65, 79, 94, 87],
"score2" : [79, 85, 79, 93, 97],
"score3" : [59, np.nan, 39, np.nan, np.nan],
"weight" : [5.43, 0.12, 10.44, 9.33, 4.22],
"diff" : [-2.1, 5, 2, -5.4, -3.3],
"place" : ["A", 'B', 'A', 'A', 'B']}
)
data
데이터를 생성해주었다.
data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 5 entries, 0 to 4
Data columns (total 6 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 score1 5 non-null int64
1 score2 5 non-null int64
2 score3 2 non-null float64
3 weight 5 non-null float64
4 diff 5 non-null float64
5 place 5 non-null object
dtypes: float64(3), int64(2), object(1)
memory usage: 368.0+ bytes
data.describe()
score1 score2 score3 weight diff
count 5.00000 5.000000 2.000000 5.000000 5.000000
mean 84.80000 86.600000 49.000000 5.908000 -0.760000
std 13.38656 8.173127 14.142136 4.148128 4.200357
min 65.00000 79.000000 39.000000 0.120000 -5.400000
25% 79.00000 79.000000 44.000000 4.220000 -3.300000
50% 87.00000 85.000000 49.000000 5.430000 -2.100000
75% 94.00000 93.000000 54.000000 9.330000 2.000000
max 99.00000 97.000000 59.000000 10.440000 5.000000
describe () 는 기술통계 정보를 알려준다.
평균 (한 변수)
# 한 변수의 평균
print('한 변수', data['score1'].mean())84.8
평균 (전체)
# 데이터 프레임 전쳉의 평균
print('전체 : ')
print(data.mean())
절사평균
절사평균은, 가장 크고 작은 값을 일정한 비율로 삭제해서 평균을 내는 것이다.
우리는 여기서 score2 의 평균을 냈고, 제일 큰 10% 값, 제일 작은 10% 값을 잘라내고 평균을 냈다.
# 절사평균
from scipy.stats import trim_mean
print(trim_mean(data['score2'],0.1))
가중평균
가중치를 해서 평균을 낸다.
# 가중 평균
np.average(data['score2'], weights=data['weight'])
중앙값 median()
# 중앙값
## 데이터 개수 : 홀수
print(data['score2'].median())## 데이터 개수 : 짝수
x = [100, 600, 100, 200, 400, 500]
print(np.median(x))결과값 : 300
최빈값 mode()
# 최빈값
data['score2'].mode()
산포도
# 산포도
data['score2'].max() - data['score2'].min()
분산과 표준편차
# 분산
print(data['score2'].var())
# 표준편차
print(data['score2'].std())분산 var()
표준편차 std()
사분위수 범위(IQR)
print(data['score2'].quantile(0.75) - data['score2'].quantile(0.25))quantile(0.25) 등으로 사분위수를 알 수 있다.
0.25는 25%,
quantile(0.75) 는 75% 이다.
0.75 사분위수 - 0.25 사분위수 = IQR = 사분위수 범위이다.
변동계수 (CV)
# 변동 계수
cv1 = data['score1'].std() / data['score1'].mean()
cv2 = data['score2'].std() / data['score2'].mean()
print('score1 의 cv계수 : ', format(np.round(cv1, 3)))
print('score2 의 cv계수 : ', format(np.round(cv2, 3)))score1 의 cv계수 : 0.158
score2 의 cv계수 : 0.094
변동계수는 표준편차에 평균을 나눈 값이다.
표준편차에 평균을 나눔으로서 평균을 기준으로 표준편차를 표준화 시켜주는 것이다.
시각화
# 시각화 패키지
%matplotlib inline
import warnings
warnings.simplefilter(action = 'ignore', category = FutureWarning)
import matplotlib.pyplot as plt
import seaborn as sns
# 깨짐 방지를 위한 Font 지정
import os
if os.name =='nt' :
font_family = "Malgun Gothic"
else :
font_family = "AppleGothic"
# 값이 깨지는 문제 해결을 위해 파라미터값 설정
sns.set(font=font_family, rc = {"axes.unicode_minus" : False})
필요한 라이브러리 import
왜도 (Skewness) 산출
왜도란, 기울어져 있는 것을 말한다. (평균보다 치우처져있는 것)
왜도 > 0 이면 왼쪽으로 치우치고, 왜도 < 0 이면 오른쪽으로 치우친다.
# 왜도 산출
from scipy.stats import skew
skew_list1 = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 4, 5]
skew_list2 = [1, 2, 3 ,3, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6]
print(skew(skew_list1))
print(skew(skew_list2))1.6656293067949786
-1.0422210554570965
산출해낸 왜도를 시각화해보자.
# 왜도 시각화
plt.figure(figsize = (12,6))
plt.subplot(1, 2, 1)
dis_plot = sns.distplot(skew_list1)
plt.title('우측 꼬리 분포, 왜도 > 1', fontsize = 16)
plt.subplot(1,2,2)
dis_plot = sns.distplot(skew_list2)
plt.title('좌측 꼬리 분포, 왜도 < 1', fontsize = 16)
plt.show()
subplot 참조. 여러 개의 그래프를 한 줄에 보여줄 수 있도록 한다.
figsize = (가로길이, 세로길이) .
그래프 사이즈를 의미한다.
sns.displot 은 seaborn 패키지를 이용하여 히스토그램을 그리는 것이다.
distplot(skew_list1) 는 skew_list1 위에서 구한 왜도를 히스토그램으로 표시해주는 것이다.

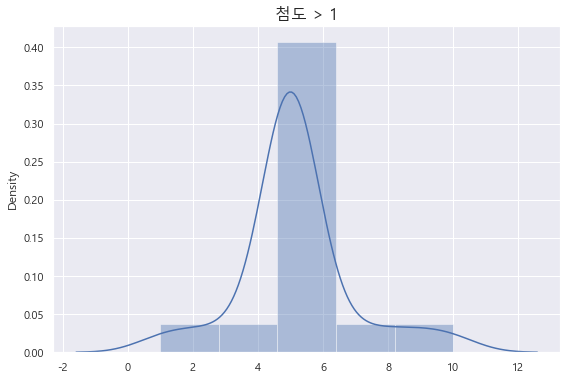
첨도 (Kurtosis) 산출
첨도란 뾰족한 정도, 평균에 데이터가 몰려있는 정도이다.
첨도가 0보다 크면 뾰족하고,
첨도가 0보다 작으면 완만하다.
# 첨도 산출
from scipy.stats import kurtosis
kur_list1 = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
kur_list2 = [1, 2, 3, 4, 5, 5, 5, 5, 5, 5, 5, 5,5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 7, 8, 9, 10]
print(kurtosis(kur_list1))
print(kurtosis(kur_list2))-1.2242424242424244
2.351887069895106
첨도가 -1, 2가 나왔다.
각각 시각화해보자.
# 첨도 시각화
plt.figure(figsize = (20, 6))
plt.subplot(1,2,1)
dis_plot = sns.distplot(kur_list1)
plt.title('첨도 < 1', fontsize = 16)
plt.show()
plt.subplot(1,2,2)
dis_plot = sns.distplot(kur_list2)
plt.title('첨도 > 1', fontsize = 16)
plt.show()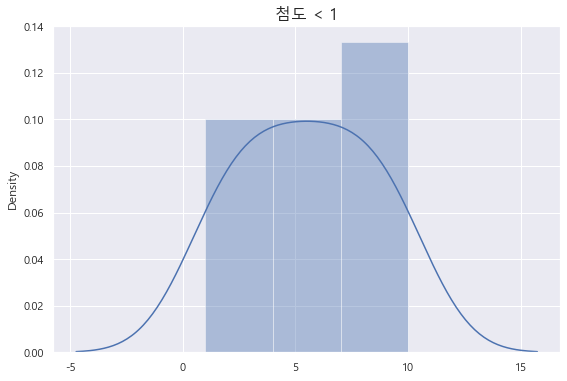
'Data Science > 통계' 카테고리의 다른 글
| [Python/statistics] 카이제곱 검정(Chi Square test , 교차분석) (2) | 2022.07.30 |
|---|---|
| 통계 기초 이론 (2) (2) | 2022.06.20 |
| 통계 기초 이론 (1) (0) | 2022.06.19 |
| R로 배우는 통계 기초 이론 (0) | 2022.06.18 |




