| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- SQL
- 공공빅데이터청년인턴
- Keras
- 공빅데
- 텍스트마이닝
- 공빅
- data
- 분석변수처리
- 클러스터링
- decisiontree
- 공공빅데이터청년인재양성
- textmining
- machinelearning
- NLP
- 2023공공빅데이터청년인재양성
- DeepLearning
- ADsP3과목
- 데이터전처리
- ADSP
- 빅데이터
- 2023공공빅데이터청년인재양성후기
- 오버샘플링
- 데이터분석
- ML
- 2023공빅데
- DL
- k-means
- 머신러닝
- datascience
- Kaggle
- Today
- Total
愛林
[Python/ML] 음성 데이터 분석(Sound Processing) - (2) 본문
음성 데이터 분석 (Sound Processing)
https://wndofla123.tistory.com/94
[Python/DL] 음성 데이터 분석(Sound Processing) - (1)
음성 데이터 분석 (Sound Processing) 소리는 공기를 구성하는 입자들이 진동하며 만들어내는 현상이다. 정확하게 정의하자면, 어떠한 물체 또는 매질(Object)의 진동으로 인해 공기 입자들이 밀고 당
wndofla123.tistory.com
이전 글에서는 음성 데이터에 대한 간단한 소개와 기본적인 음파의 개념, wave 파일에 대해서
간략하게 말해보았었다.
이번에는 음성 파일 데이터에서 특징(Feature) 를 추출하는 방법인 푸리에 변환(Fourier transform) 과
스펙트럼(Spectrum), MFCC 에 대해서 알아보자.
정현파 조합 (Sinusolida Signal)
모든 신호는 주파수(Frequency) 와 크기(Magnitude), 위상(Phase) 이 다른 정현파(Sinusolida Signal) 의 조합으로
나타낼 수 있다. Fourier 변환 (퓨리에 변환)은 조합된 정현파의 합 (이를 하모니라고 한다) 신호에서 그 신호를 구성하는
정현파들을 분리해내는 방법이다.
한 마디로 말하자면, 우리가 듣는 소리신호는 각기 다른 단일 주파수로 이루어져 있는데,
이 단일 주파수를 정현파라고 한다. 이것들이 합쳐지면 우리가 듣는 소리가 된다.
마치 내가 이전 시간에 복수의 single tone 들을 모아서 화음(Harmony) 를 만들어낸 것과 비슷하다고 보면 된다.
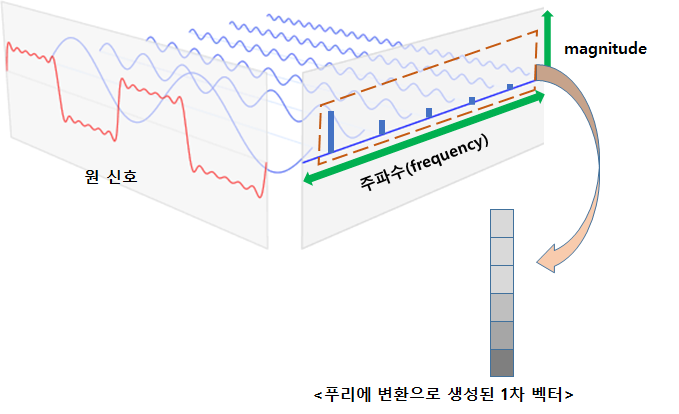
해당 내용을 찾아보다가 이를 완전히 직관적으로 보여주는 시각화 그림을 찾았다.
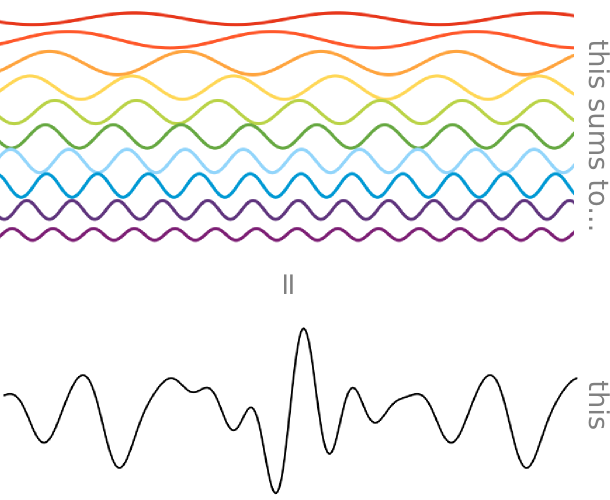
위쪽의 무지개 색을 가진 단일 정현파들이 모여서 아래와 같은 소리를 만들어내는 것이다.
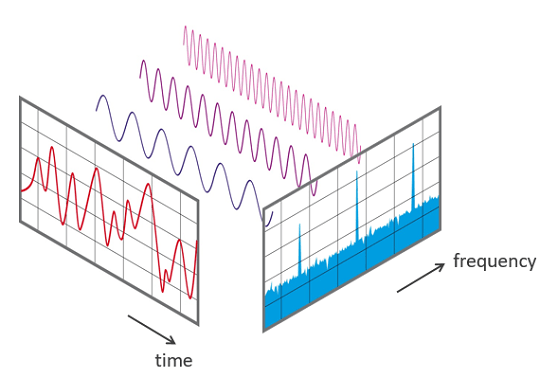
내가 보기엔 이보다 정현파를 잘 설명하는 그림은 없다.
N = 1024
T = 1.0 / 44100.0
f1 = 697
f2 = 1209
t = np.linspace(0.0, N*T, N)
y1 = 1.1 * np.sin(2 * np.pi * f1 * t)
y2 = 0.9 * np.sin(2 * np.pi * f2 * t)
y = y1 + y2
plt.subplot(311)
plt.plot(t, y1)
plt.title(r"$1.1\cdot\sin(2\pi\cdot 697t)$")
plt.subplot(312)
plt.plot(t, y2)
plt.title(r"$0.9\cdot\sin(2\pi\cdot 1209t)$")
plt.subplot(313)
plt.plot(t, y)
plt.title(r"$1.1\cdot\sin(2\pi\cdot 697t) + 0.9\cdot\sin(2\pi\cdot 1209t)$")
plt.tight_layout()
plt.show()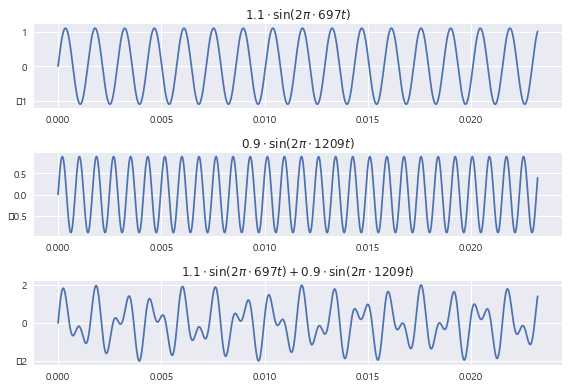
코드를 통해 확인해보았다. 1번째 sin 그래프와 두번째 sin 그래프를 더하여 아래쪽의 소리 그래프가 나왔다.
퓨리에 변환 (Fourier Transform)
오일러 공식을 통해 지수부가 허수인 복소 지수함수(Complex exponential function) 은 cos함수인 실수부와 sin함수인 허수부의 합으로 나타낸다.
exp(i⋅x)=cosx+isinx
다음은 주기가 T이고 주파수가 2π/T 인 복소 지수함수이다.
주기가 T인 sin 과 cos의 조합이 된다.

x대신에 2π/T 가 들어갔다.
따라서 주기가 T/n 이고 주파수가 n*2π/T 인 복소 지수함수는 다음과 같다.

이렇게 주기 T를 가지고 반복되는 모든 함수 y(t) 는 주파수와 진폭이 다른 몇 개의 sin함수 (정확히는 복소 지수함수) 의 합으로 나타낼 수 있다.
이 sin 함수의 진폭을 구하는 과정을 퓨리에 변환(Fourier Transform) 이라고 한다.
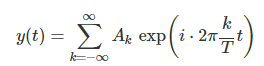
이 식에서 k번째 sin함수의 진폭은 다음 식으로 계산한다. 이것이 퓨리에 변환이다.
어렵지 않다. 그냥 오른쪽 식을 Ak만 남기고 모두 왼쪽으로 보내면 되는 것이다.
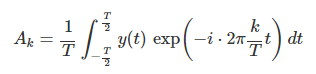
그냥 sin 함수의 진폭을 구하는 것이 퓨리에 변환값이라는 멋진 이름이 된다.
이런 퓨리에 변환을 하는 이유는 우리가 위에서 말했던 Harmony가 어떤 정현파의 조합으로 구성이 되어있는 지를
분해해서 확인하기 위해서이다. 시계열 데이터를 주파수 영역으로 변환한다.
뭐든지 분석을 위해서는 복잡한 어떤 것을 최대한 단순한 어떤 것으로 바꾸는것이 중요하다.
이산 퓨리에 변환 (Discrete Fourier Transform, DFT)
이산 퓨리에 변환은 DFT 라고도 부르며, 길이가 N인 이산시간 시계열 데이터가 있을 때,
이 이산시간 시계열이 주기 N으로 계속 반복된다고 가정하여 퓨리에 변환을 한 것이다.
이 때 원래의 이산시간 시계열 데이터는 다음 주파수와 진폭이 다른 N개의 sin함수 값으로 나타난다.
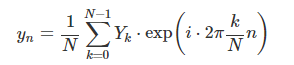
이를 진폭 Yk 만 남기고 모두 옆으로 보내면
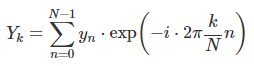
퓨리에 변환값을 구한 것이다.
그냥 sin 함수의 진폭을 구하면 그게 그냥 퓨리에 변환값이라는 멋진 이름을 갖는 것이다.
이 sin 함수들의 진폭들과 나머지 정보들이 소리를 이루는 정현파들의 특징 벡터가 된다.
고속 퓨리에 변환 (Fast Fourier Transform, FFT)
고속 퓨리에 변환 ,FFT는 아주 적은 계산량으로 DFT를 하는 알고리즘을 말한다.
길이가 2^N인 시계열에만 적용할 수 있다는 단점이 있지만, 보통의 DFT가 O(N^2) 수준의 계산량을 요구하는 데
반해 FFT는 O(Nlog2N) 계산량으로 DFT를 구할 수 있다.
사실상 그냥 빠르게 퓨리에 변환을 하는 것과 같다. 짧은 시간 단위로 쪼갠 뒤 퓨리에 변환을 해준다.
바꾸는 방식은 아래와 같다.

실제로는 다음과 같이 계속 반복되는 시계열에 대해서 퓨리에 변환을 한다.
따라서 시계열의 시작 부분과 끝 부분이 너무 다르면 원래 시계열에는 없는 신호가 생기는
깁스 현상(Gibbs Phenomenon) 이 발생할 수 있다.
y2 = np.hstack([y, y, y])
plt.subplot(211)
plt.plot(y2)
plt.axvspan(N, N * 2, alpha=0.3, color='green')
plt.xlim(0, 3 * N)
plt.subplot(212)
plt.plot(y2)
plt.axvspan(N, N * 2, alpha=0.3, color='green')
plt.xlim(900, 1270)
plt.show()
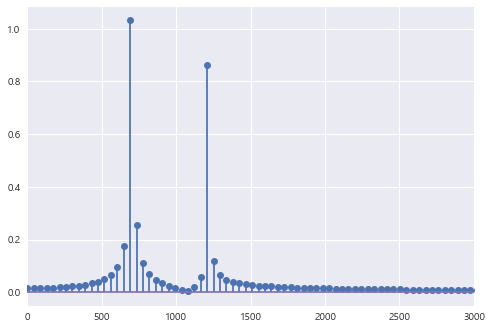
scipy 패키지의 fftpack 서브 패키지에서 제공하는 fft 명령으로 이 신호에 담겨진 주파수를 분석하면
다음과 같이 692Hz와 1211Hz 성분이 강하게 나타난다.
이와 같은 plot 을 피리오도그램(Periodogram) 이라고 한다.
from scipy.fftpack import fft
yf = fft(y, N)
xf = np.linspace(0.0, 1.0/(2.0*T), N//2)
plt.stem(xf, 2.0/N * np.abs(yf[0:N//2])) # stem은 줄기잎그림
plt.xlim(0, 3000)
plt.show()
이산 코사인 변환 DCT (Discrete Cosine Transform)
DCT는 DFT와 유사하지만 기저함수로 복소 지수함수가 아닌 코사인 함수를 사용한다.
DFT보다 계산이 간단하고 실수만 출력한다는 장점이 있어서 DFT 대용으로 많이 사용된다.
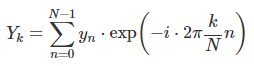
위에서 살펴본 DFT의 수식이다.
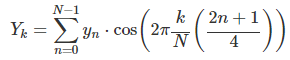
DCT 의 수식이다.
비슷하지만 cos 을 사용하는 것을 확인할 수 있다.
from scipy.fftpack import dct # 2차원 이산 코사인 변환
dct_type = 2 # dct 타입
yf2 = dct(y, dct_type, N) # dct(입력배열, dct타입, N=정수. 선택사항)
plt.subplot(311)
plt.stem(np.real(yf))
plt.title("DFT 실수부")
plt.subplot(312)
plt.stem(np.imag(yf))
plt.title("DFT 허수부")
plt.subplot(313)
plt.stem(np.abs(yf2))
plt.title("DCF")
plt.tight_layout()
plt.show()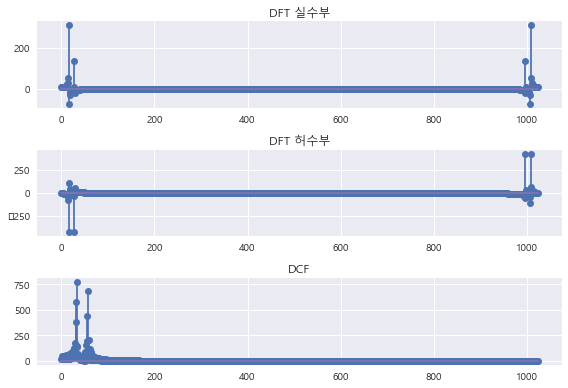
실수부가 cos. 허수부가 sin 이다.
DCF 그래프를 확인해보면 모두 실수인 것을 확인할 수 있다.
스펙트럼 (Spectrum)
스펙트럼이란, 각 주파수의 정도를 시각화해서 보여주는 방법이다.
정확한 명칭은 파워 스펙트럼 (Power Spectrum) 또는 스펙트럼 밀도 (Spectrum Density) 이다.
퓨리에 변환은 결정론적인 시계열 데이터를 주파수 영역으로 변환하는 것을 말하지만,
스펙트럼 (Spectrum) 은 확률론적인 확률과정(Random Process) 모형을 주파수 영역으로 변환하는 것을 말한다.
따라서 퓨리에 변환과 달리 시계열의 위상(Phase) 정보는 스펙트럼에 나타나지 않는다.
그 말은 즉, 파형은 시간에 흐름에 따라 변화하는 time-domain 의 성질을 띄지만,
스펙트럼은 각 frequency(주파수) 마다 그 정도가 달라지는 frequency-domain 의 성질을 띄므로,
시간의 변화에 따른 정보는 유실된다.
근데 다들 스펙트럼이 퓨리에 변환을 하면 나오는 값이라고 해서 헷갈리기 시작한다.

스펙트럼을 추정할 때 사용하는 방법 중의 하나는 전체 시계열을 짧은 구간으로 나눈 뒤
깁스 현상을 줄이기 위하여 각 구간에 윈도우(window)를 씌우고 FFT 계산으로 나온 값을 평균하는 방법이다.
보통은 log scale 로 표현된다.
import scipy as sp
import scipy.signal
f, P = sp.signal.periodogram(y, 44100, nfft=2**12)
plt.subplot(211)
plt.plot(f, P)
plt.xlim(100, 1900)
plt.title("선형 스케일")
plt.subplot(212)
plt.semilogy(f, P)
plt.xlim(100, 1900)
plt.ylim(1e-5, 1e-1)
plt.title("로그 스케일")
plt.tight_layout()
plt.show()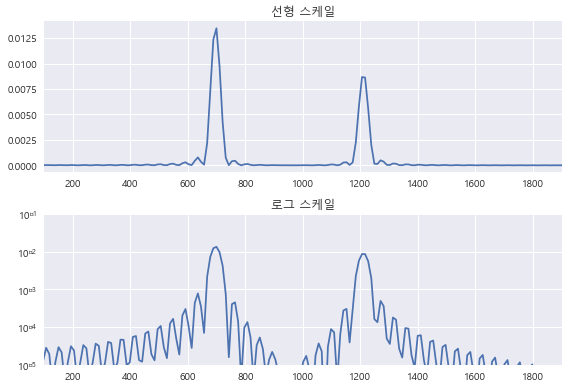
STFT (Short - Time Fourier Transform)
STFT 는 퓨리에 변환의 한계를 보완하는 방법이다.
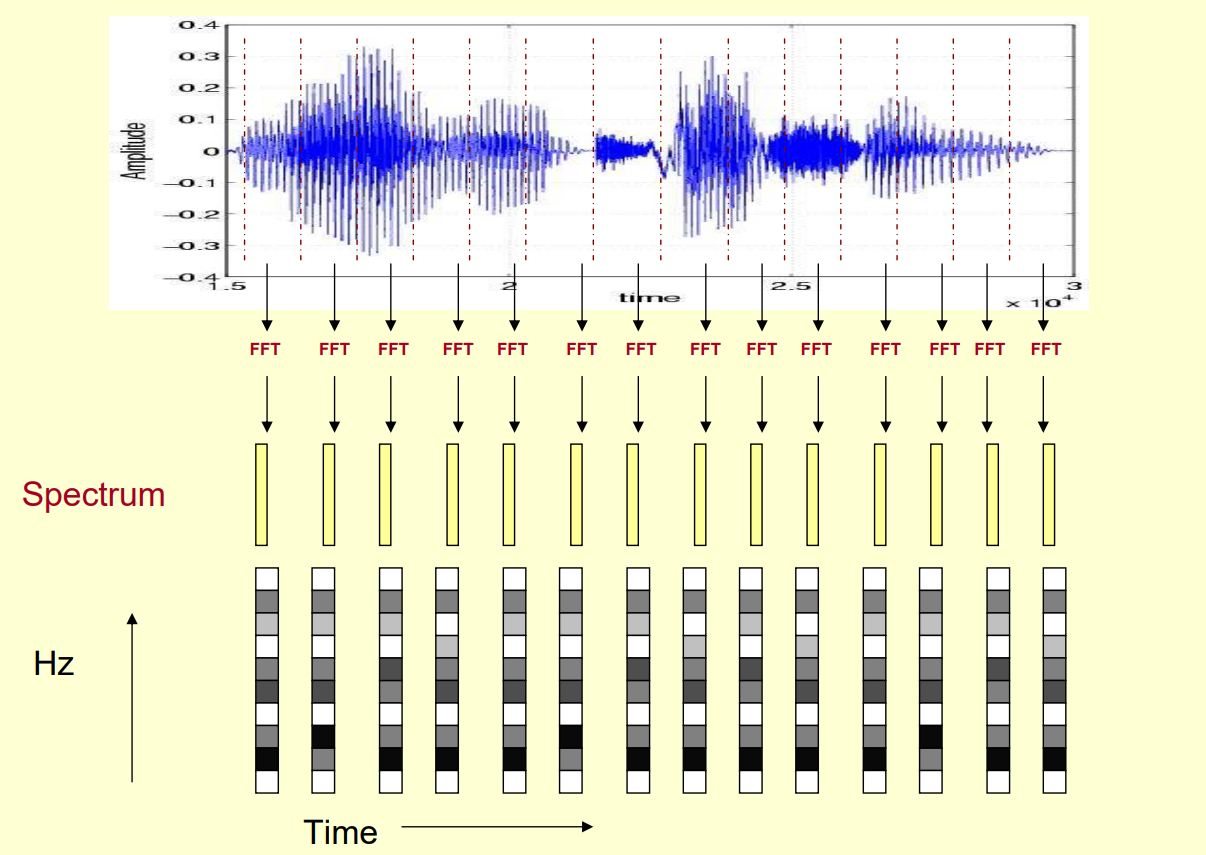
STFT 는 전체 길이보다는 짧은 어떠한 시간 간격(window) 을 설정한 후, 이 간격을 시간의 흐름에 따라
움직여가며 복수 변환(Fast 퓨리에 변환) 을 행하고, 시간에 흐름에 따른 주파수 정보를 얻는다.
시간, 주파수의 2차원 데이터로 나타낸다.
9초의 소리가 있다면, 이를 1초 단위로 쪼개고 1초 간격으로 퓨리에변환을 한다.
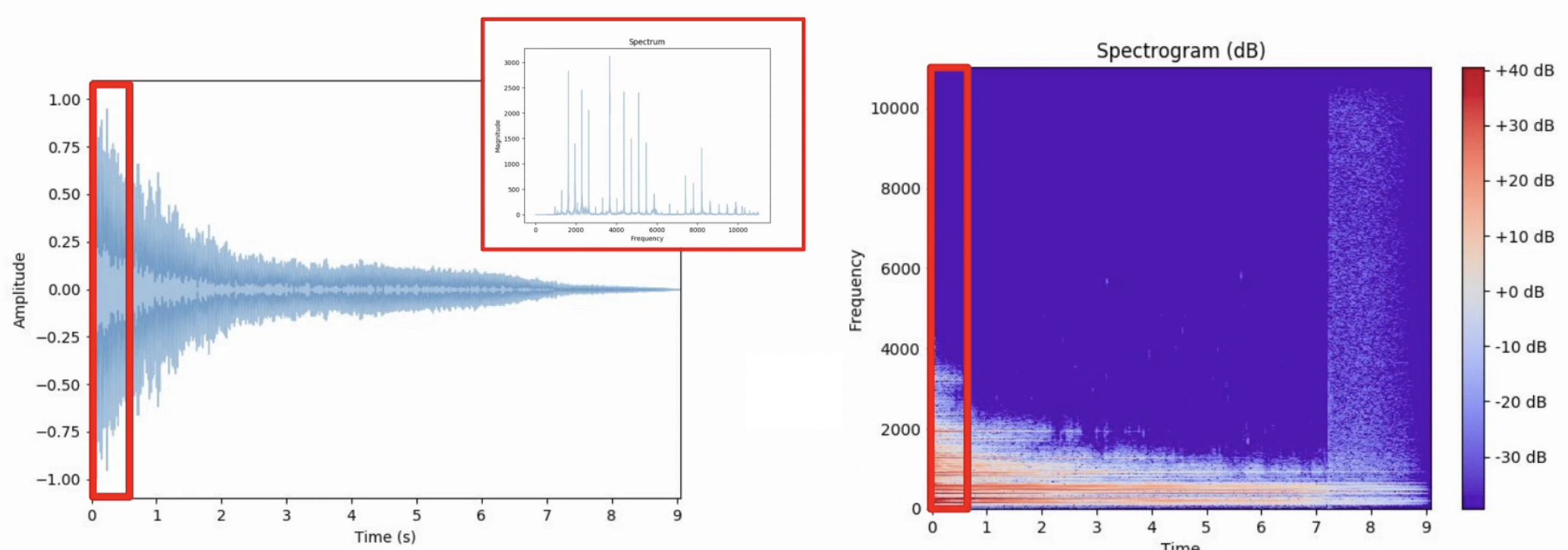
STFT 를 행한 후 그 산출물은 주파수, 진폭 그리고 시간 정보까지 포함된
Spectogram(스펙토그램)이다.
아래처럼 시각화하여 나타낼 수 있다. X축은 시간, Y축은 주파수, 그리고 그 주파수의 정보가 데시벨(색깔)로 표현됐다.
Librosa 패키지
파이썬이 강력한 프로그래밍 언어인 이유는 바로 라이브러리가 다 만들어져 있다는 것이다.
파이썬으로 STFT 스펙트럼 분석 뿐만 아니라 다양한 음성 데이터 처리를 할 때 librosa 를 이용한다.
librosa로 다양한 wav파일들의 파형을 처리할 수 있을 뿐만 아니라 , FFT나 MFCC등도 가능하다.
jupyter Notebook 환경에서 librosa 패키지를 이용할 때에는 jupyter_notebook_config.py 파일의
iopub_data_rate_limit 설정을 10000000 정도로 크게 해야 한다.
import librosa
import librosa.display
D = np.abs(librosa.stft(y)) #stft
librosa.display.specshow(librosa.amplitude_to_db(D, ref = np.max), y_axis = 'linear',
x_axis = 'time') # 시각화
plt.title("Dual Tone")
plt.ylim(0,4000)
plt.show()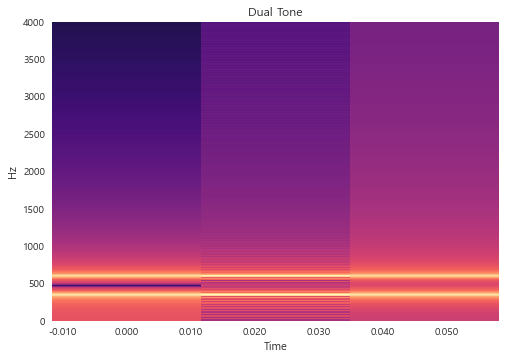
import scipy.io as sio
from scipy.io import wavfile
sr_octave, y_octave = sp.io.wavfile.read("octave.wav")
D_octave = np.abs(librosa.stft(y_octave))
librosa.display.specshow(librosa.amplitude_to_db(D_octave, ref=np.max), sr=sr_octave, y_axis='linear', x_axis='time')
plt.title('Octave')
plt.ylim(0, 2000)
plt.show()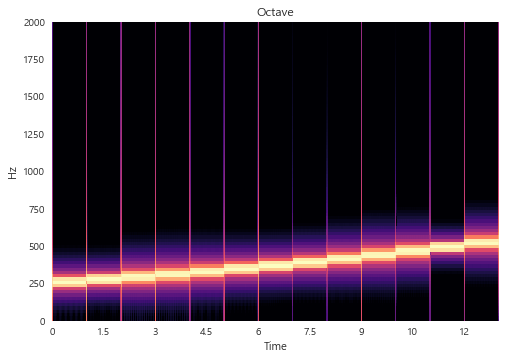
이전 게시글에서 만든 octave 파일을 STFT 해보았다.
스펙토그램은 복소수로 return 되기 때문에, np.abs 를 사용하여 amplitude(진폭) 로 바꾸어주고,
스펙토그램을 DB scale 로 바꾸어주기 위해 librosa.amplitude_to_db 를 사용해준다.

Octave.wav 파일은 C Note 부터 점점 올라가는 노트였는데,
해당 주파수(freq) 들이 적절하게 잘 시각화된 것을 확인할 수 있다.
MFCC (Mel Frequency Cepstral Coefficient)
실제 소리를 분석할 때는 퓨리에 변환 뿐만 아니라 그 외에 차원을 축소하거나 다른 분석에 용이한
특징을 추출하는 과정인 Feature Extraction 을 거친다.
특히 소리 신호에서 많이 사용되는 소리 데이터의 Feature 로는 MFCC가 있다.
MFCC는 갖가지 신호가 합쳐져서 생성된 소리가 가지는 고유한 특징을 추출한 값이다.
이를 이해하기 위해서는 Mel-Spectogram 과 Mel-scale에 대한 이해가 필요하다.
멜 스펙토그램 (Mel-Spectogram) 이란, 사람의 달팽이 관의 특성을 반영한 Mel-scale 을 적용한
스펙토그램 표현법이다. 달팽이관은 저주파 대역을 감지하는 구간이 조밀하고,
고주파 대역을 감지하는 구간은 넓게 이루어져 있다.
따라서 저주파 대역에 의미있는 정보가 많이 집중되어 있으며, 인간의 청각은 저주파 대역에서
더 민감한 반응을 한다는 점을 반영해서 주파수의 대역에 차등적으로 중요도를 적용하는
Mel-Scale 이라는 것이 제안되었다.
다음 공식에 따라 Mel unit. 멜 단위로 스펙트럼의 주파수 단위를 바꿀 수 있다.
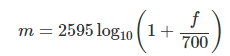
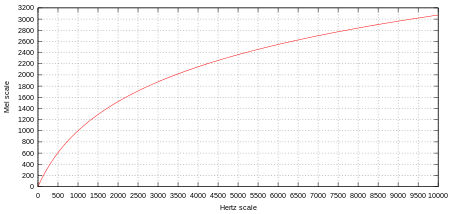
위에서 STFT 를 진행해보았던 Octave 파일을 Mel 단위로 바꾸어 보았다.
S_octave = librosa.feature.melspectrogram(y=y_octave, sr=sr_octave, n_mels=128)
librosa.display.specshow(librosa.power_to_db(S_octave, ref=np.max), sr=sr_octave, y_axis='mel', x_axis='time')
plt.ylim(0, 4000)
plt.show()
MFCC는 Mel Scale 로 바꾼 Spectrum을 40개의 주파수 구역(band) 로 묶는다.
이렇게 퓨리에 변환을 수행하여 나온 스펙토그램을 Mel-scale 을 기반으로 하여 나눈 것을 Filter Bank라고 한다.
그리고 이 필터뱅크에 로그변환을 수행하면 Mel-sclae에 따라 나누어진 구간(band) 별로 분포 정보를 확보할 수 있다.
이렇게 로그 변환한 Log Mel-Spectogram에 역퓨리에 변환을 적용하면 Cepstrum이라는 스펙트럼의 특성값.
소리의 대표적인 특징을 추출해낼 수 있다.
이렇게 구한 결과의 진폭(amplitude) 을 구하면 그것이 소리의 대표적 특징인 MFCC이다.
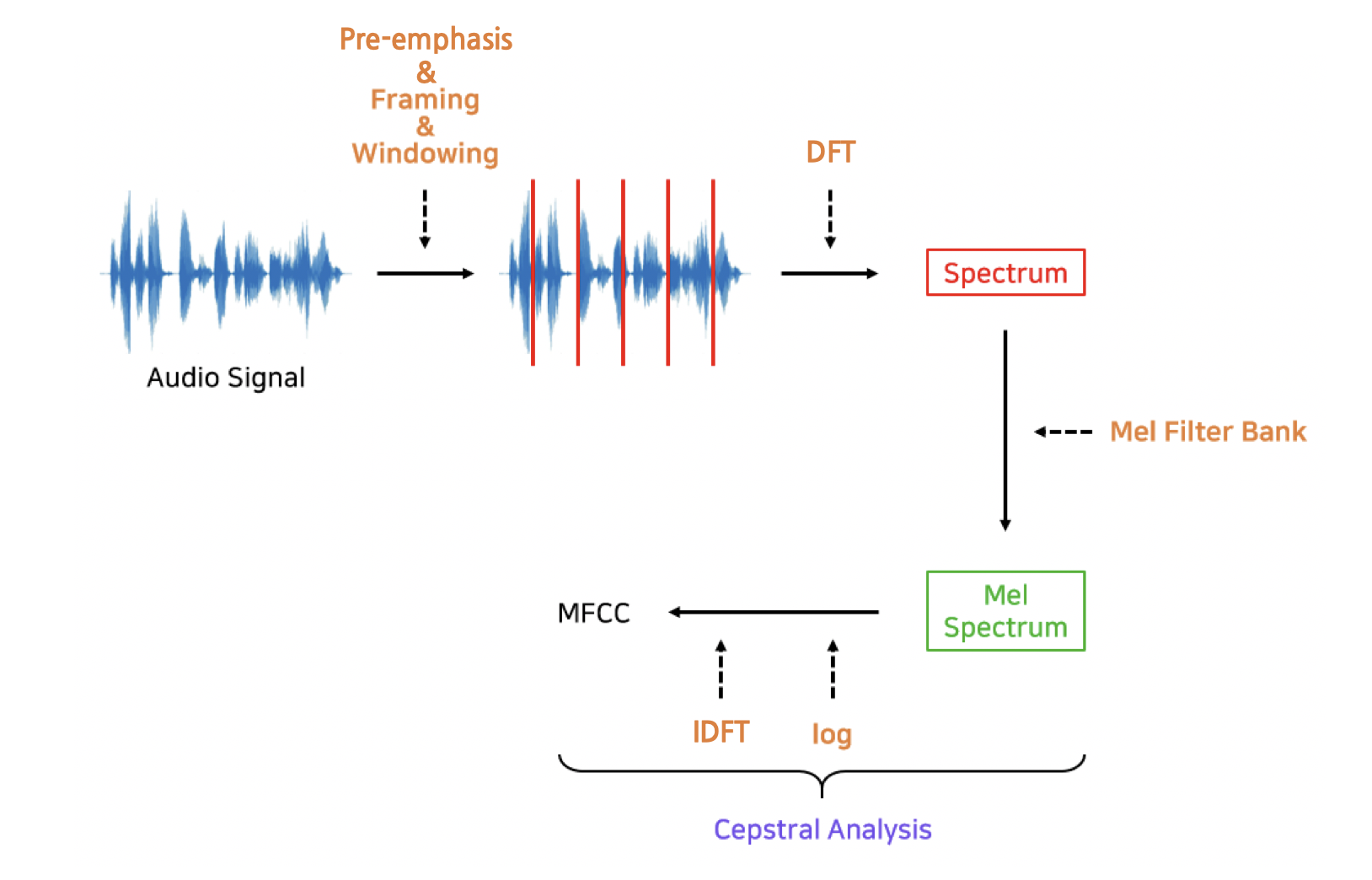
그냥 MFCC를 간단하게 설명하자면,
여러개의 정현파들로 구성된 소리를 쪼개서 특징적인 부분을 추출해낸 뒤 (퓨리에 변환, STFT),
이를 사람의 귀의 특성에 맞추어 변형시켜준다(Mel Scale).
그리고 여기서 또 더 특징적인 부분을 추출해낸(역퓨리에 변환으로 얻어낸 Cepstrum)
Feature 가 MFCC라고 볼 수 있다.
그렇다.
간단하게 이를 확인해보자.
y, sr = librosa.load(librosa.util.example('vibeace'), offset = 30, duration = 5)
plt.plot(y[1000:5000])
plt.show()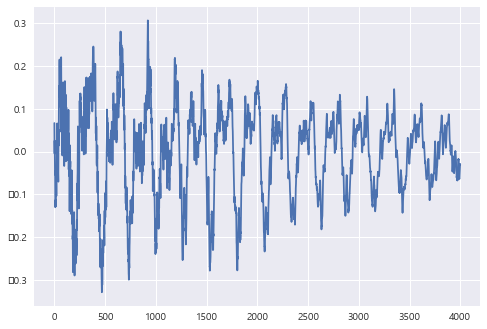
Librosa에서 제공하는 기본적인 example 파일을 가져와서 시각화해주었다.
위와 같은 형태의 waveform 을 띄고 있음을 확인할 수 있다.
from IPython.display import Audio, display
Audio(y, rate = sr)
오디오도 들을 수 있다.
흥겹다.
S = librosa.feature.melspectrogram(y=y, sr=sr, n_mels=128, fmax = 8000)
librosa.display.specshow(librosa.power_to_db(S, ref=np.max), sr=sr, y_axis = 'mel',
x_axis = 'time')
plt.show()
melspectogram을 통해 melspectogram 을 그려보았다.
n_mels 는 주파수 해상도를 결정하는 파라미터이다.
아래쪽은 시간, 옆쪽은 Hz 주파수를 표현하였다.
이걸로 MFCC를 추출해보자.
librosa의 mfcc 를 사용한다.
n_mfcc 는 압축을 얼마나 할 지에 대한 파라미터인데 , 크면 클수록 스펙토그램의 값을 더 잘 담아낸다고
볼 수 있다. 적을수록 손실이 많이 발생한다.
# MFCC
mfccs = librosa.feature.mfcc(y=y, sr=sr, n_mfcc = 40) # n_mfcc 압축을 얼마나 할 지.
librosa.display.specshow(mfccs, x_axis = 'time')
plt.title("MFCC")
plt.tight_layout()
plt.show()
위에서 시각화한 melspectogram의 특징적인 부분 (밝은 부분) 쪽이
시각화 된 것을 확인할 수 있다.
Review
모든 음성은 주파수, 크기, 위상으로 이루어진 정현파의 조합으로 이루어져 있다.
음성을 분석하기 위해서 퓨리에 변환(Fourier Transform) 을 사용하여 복소 지수함수로 이루어진 함수의
sin 함수 진폭을 구한다.
퓨리에 변환을 빠르게 진행하는 FFT가 있다.
퓨리에 변환으로 스펙트럼을 얻을 수 있는데, 이는 시간의 흐름에 따른 변화를 보여주지 못한다는 한계가 있다.
그런 한계를 극복하기 위해 사용하는 방법이 STFT 이다.
STFT로 주파수와 진폭 그리고 시간 정보까지 포함되어 있는 정보를 스펙토그램이라고 한다.
이 스펙토그램을 사람이 들을 수 있는 주파수로 변형시켜주는 것이 Mel Scale 변환이다.
Mel scale 변환을 시켜준 후 이를 또 Log 변환한 후 역퓨리에 변환을 하면 Cepstrum이라는 것을 얻을 수 있는데,
이것이 소리의 특징적인 부분이기 때문에 소리의 Feature가 된다.
이렇게 얻어낸 Feature 를 MFCC라고 한다.
Python 에서는 Librosa 패키지를 이용하여 이런 음성 데이터를 분석할 수 있다.
음성 데이터는 처음 다루어보는데, 복잡해보인다.
참고
푸리에 변환과 스펙트럼 — 데이터 사이언스 스쿨
.ipynb .pdf to have style consistency -->
datascienceschool.net
↓ 제일 설명이 잘 되어있다!
https://lucaseo.github.io/posts/2020-12-13-understanding-audio-data-sound-waveform-adc/
[KR] ML/DL을 위한 소리 데이터 이해하기(1) - Waveform, ADC
1. 소리 데이터란 소리는 다음 과정에서 생산된 것을 의미합니다. (1) 어떠한 물체 또는 매질(object)의 진동(vibration)으로 인해 공기 입자들이 밀고 당겨지는 반복적인 과정(oscilation)에서 생긴 파동(
lucaseo.github.io
https://hyongdoc.tistory.com/401
[Python 음성 데이터 분석] Librosa 라이브러리를 이용한 주파수 분석
이번 포스팅에서는 지난 포스팅에 이어, 실제로 파이썬을 이용해 어떻게 음성 데이터를 불러오고 가공하는지에 대해 알아보겠습니다. Librosa 라이브러리 만든이 칭찬해~~ 파이썬은 배워두면 참
hyongdoc.tistory.com
https://www.clairvoyant.ai/blog/music-genre-classification-using-cnn
Music Genre Classification Using CNN
Example of Deep Learning to analyze audio signals to determine the music Genre Convolutional Neural Networks.
www.clairvoyant.ai
https://everyday-tech.tistory.com/5
[2탄] 딥러닝 음성 인식 - 디지털 신호의 특징 추출
everyday-tech.tistory.com
'Data Science > Machine Learning' 카테고리의 다른 글
| [Python/ML] Outlier Detection :: Pyod Library (3) | 2023.01.19 |
|---|---|
| [Python/ML] 이상 탐지 (Anomaly Detection) (2) | 2022.12.21 |
| [Python/ML] 음성 데이터 분석(Sound Processing) - (1) (3) | 2022.12.19 |
| [Python/ML] 분류 알고리즘 (Classification Algorithm) : 로지스틱 회귀 (Logistic Regression) (확률적 판별 모델) (2) | 2022.09.06 |
| [Python/ML] 분류 알고리즘 (Classification Algorithm) : 나이브 베이즈 (Naive Bayes) (2) | 2022.08.31 |




