[Python/Data Analysis] Mall_Customer 데이터를 이용한 Clustering 실습 : EDA, 계층적 군집화(Hierarchical Clustering), K-means 군집화

Data Science/DATA

[Python/Data Analysis] Mall_Customer 데이터를 이용한 Clustering 실습 : EDA, 계층적 군집화(Hierarchical Clustering), K-means 군집화

愛林 2022. 8. 3. 21:29

Clustering 을 실습해보자.

Mall_Customer 데이터를 이용한 Clustering 실습

전처리(Preprocessing) & EDA

먼저, 필요한 라이브러리들을 import 해주자.

import numpy as np
import pandas as pd

import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('seaborn')
sns.set_palette("hls")

import warnings
warnings.filterwarnings('ignore')

import os
if os.name == 'nt' : # windows OS
    font_family = "Malgun Gothic"
else : #Mac OS
    font_family = "AppleGothic"
    
# 값이 깨지는 문제 해결을 위해 파라미터값 설정
sns.set(font=font_family, rc ={"axes.unicode_minus" : False})

불필요한 게 있을 수도 있다. 나는 매일매일 라이브러리는 복붙하기 때문에 ^^

데이터를 불러와준다.

mall_df = pd.read_csv('./Mall_Customers.csv')
mall_df.head()
del mall_df['CustomerID']

CustomerID 칼럼은 불필요한지 없애주었다.

깔끔한 데이터

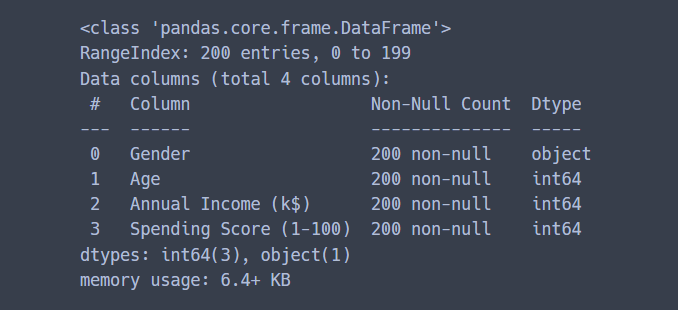
df.info(), df.shape() 를 사용해서 데이터 정보를 살펴보았다.

총 200개 데이터이고,

칼럼은 5개이다. (데이터 칼럼은 4개)

각각 ID, 성별(Gender), 나이(Age), 연간소득(Annual Income), 소비지수(Spending Score)

Gender 성별 데이터는 object 타입이므로,

미리미리 One-Hot Encoding 으로 데이터를 실수화시켜주자.

mall_df['Gender'].replace({'Male':0, 'Female':1}, inplace=True)
mall_df.head()

남자(Male) 은 0, 여자(Female) 은 1 로 바꾸어주었다.

k-means , DBSCAN 등은 거리 기반의 알고리즘이기 때문에 단위의 영향력을 제거해주기 위해서

표준화를 진행해준다.

한 가지가 너무 커지면 그 한 가지의 데이터가 클러스터링에 더 큰 영향을 미치게 되므로,

스케일링으로 각각 변수들이 비슷한 영향을 가질 수 있게 해주어야 한다.

여기서는 X-mean / Std 로 변환시켜주어서 평균이 0, 표준편차가 1로 정규화시켜주는

StandardSScaler 를 사용했다.

from sklearn.preprocessing import StandardScaler

standard_scaler = StandardScaler()
mall_scaled_df = pd.DataFrame(standard_scaler.fit_transform(mall_df), 
                              columns=mall_df.columns)

StandardScaler 에 mall_df 데이터를 피팅시켜주고, 정규화시켰다.

columns 는 mall_df 의 칼럼을 그대로 사용했다.

바꾸어준 데이터는 mall_scaled_df 에 저장했다.

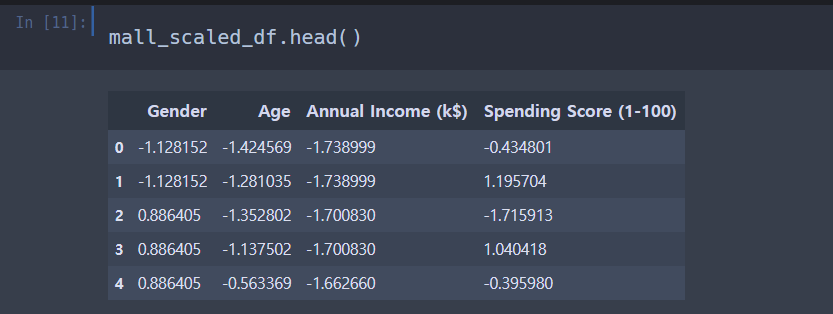
성별의 성비를 확인해보자.

matplotlib , Seaborn 을 사용하여 막대를 만들어주었다.

print('---------- 성별 성비 ----------')
print(mall_df['Gender'].value_counts() / mall_df.shape[0])
print('-------------------------------')

plt.figure(figsize=(12, 5))
sns.countplot(mall_df['Gender'], palette='Set2')
plt.xticks([0, 1], ['Male', 'Female'])

---------- 성별 성비 ----------
1    0.56
0    0.44
Name: Gender, dtype: float64
-------------------------------

여자 성비(1) 이 조금 더 많다. (56%)

밀도그래프 kdeplot 을 그려주자.

plt.figure(figsize=(12, 5))
sns.kdeplot(mall_df['Age']) # kdeplot = 밀도 그래프
print('mean   -> ', mall_df['Age'].mean())
print('median -> ', mall_df['Age'].median())

mean   ->  38.85
median ->  36.0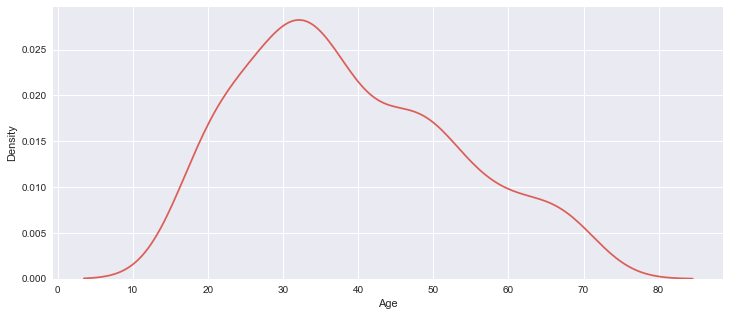

연령에 대해서 밀도그래프를 그려서 확인했다.

밀도그래프는 오른쪽이 조금 더 긴 꼬리를 갖는 형태로 만들어졌다.

30-40대의 데이터가 가장 많다.

평균 나이는 38.85 세, 중앙값은 36세이다.

이제 나이와 소득으로 scatter plot 을 그려보자.

plt.figure(figsize=(12, 5))
sns.scatterplot(x='Age', y='Annual Income (k$)', data=mall_df, hue='Gender')

별다른 소득은 없는 듯 하다.

cluster 처럼 보이는 부분은 없다.

전반적으로 나이가 증가함에 따라서 annual Income 도 증가하고, 40대 이후로부터는 annual income이

점차 감소하는 것이 보인다.

Age의 변화에 따라 Annual Income (평균소득) 의 변화를 scatter plot이 아닌 lineplot으로도 확인해보았다.

plt.figure(figsize=(12, 5))
sns.lineplot(x='Age', y='Annual Income (k$)', data=mall_df)

산점도로 확인한 것과 비슷한 결과가 나온 것 같다.

x축을 나이, y축을 소비수준(Spending Score) 로 하여 Scatter plot 을 그려보았다.

plt.figure(figsize=(12, 5))
sns.scatterplot(x='Age', y='Spending Score (1-100)', data=mall_df, hue='Gender')
plt.axvline(40, 0, 100)
plt.axhline(60, 0, 80)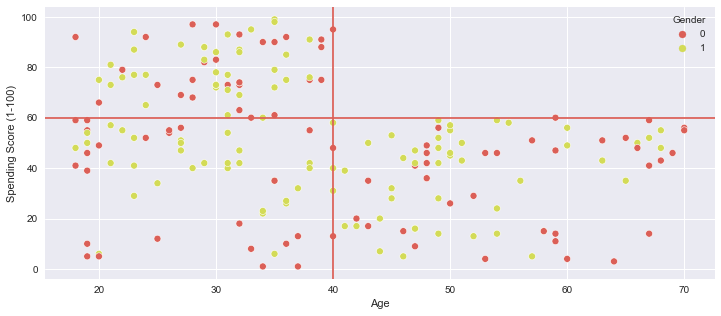

asvline 은 vertical 세로선이고,

axhline 은 horizon 수평선이다.

age가 20~40대 사이인 경우 Spending Score 의 분포가 매우 넓다.

적게 소비하는 층부터 많은 소비를 하는 층까지 다양하다. Spending Score가 높은 쪽이 조금 더 많은 것

같아보인다. 하지만 age가 40대를 넘어서면서부터 spending score 의 분포가 급격하게 줄어든다.

전반적으로 Spending Score 가 60을 넘지 않고 밑도는 것이 보인다.

이 부분에서 어느정도 Clustering 이 이루어질 수 있지 않을까 생각할 수 있다.

x 축을 평균 소득, y축을 소비지수로 하여 Scatter Plot 을 그려보았다.

연령을 그룹별로 나누어서 점 색으로 표현했다.

plt.figure(figsize=(12, 5))
sns.scatterplot(x='Annual Income (k$)', y='Spending Score (1-100)', data=mall_df, hue='Age')

여기서 5개 정도의 군집이 보이는 것 같다.

Annual income 낮고, spending score도 낮은 경우 -> 0~20대 사이
Annual income 낮고, spending score은 높은 경우 -> 20~60 사이
Annual income 보통, spending score도 보통 -> 고른 연령대
Annual income 높고, spneding score 낮은 경우 -> 40~80대 사이
Annual income 높고, spending score 높은 경우 -> 20~40대 사이

실제 데이터는 Age, Annual Income, Spending Score 총 3차원이다.

그러나 우리가 시각화한 것은 2차원이다. 따라서 3차원으로 시각화하여 보았을 때는 또 다른 군집이

보일 수도 있을 것으로 예상된다. 대략적인 전처리와 EDA 는 이정도에서 마무리해도 될 것 같다.

이제 진짜 Clustering 을 수행해서 데이터를 알아보도록 하자.

계층적 군집화 ( Hierarchical Clustering )

Hierarchical Clustering 은 중복을 허용하며 진행하는 군집화이다.

이 말은 즉슨, 군집 내에 군집이 속할 수 있다는 뜻이다.

일정 높이에서 Dendrogram을 잘라서 군집의 수를 결정한다.

Dendrogram은 클리스터링의 결과를 시각화하기 위한 대표적인 그래프이다.

덴드로 그램은 나무를 나타내는 다이어그램입니다. 이 다이어그램 표현은 다른 상황에서 자주 사용됩니다. 계층 적 클러스터링에서, 이는 대응하는 분석에 의해 생성 된 클러스터의 배열을 예시한다. 위키백과(영어)

Hiierarchical Clustering 은 군집의 개수를 모를 때 진행하게 된다.

이를 진행하면 데이터가 Dendrogram 으로 나타나게 되는데,

이를 사용해서 군집의 개수를 정하게 된다.

거리를 측정하는 방법은

L1 norm (manhattan distance,맨해튼 거리) , L2 norm (euclidean distance,유클리드 거리),

mahalanobis (feature간의 공분산 행렬을 고려한 거리), corr distance (상관계수 거리, 상관계수 높을수록 거리 짧게)

가 있다.

보통 맨해튼 거리와 유클리드 거리를 가장 많이 사용한다.

유클리드 거리는 그냥 최단거리이다. 초록색 선을 보면 된다.

맨해튼 거리는 현실적인 거리이다.

파란색, 노란색, 빨간색 선은 모두 길이가 같다.

이 길이가 바로 바로 맨해튼 거리이다.

현실적인 거리라는 것이다 .

x값의 차와 y값의 차를 각각 절대값으로 바꾸어서 합한 값이 맨해튼 거리이다.

군집 간의 거리를 측정하는 방법은

single linkage (군집 간 element끼리의 거리 중 min을 군집 간 거리로 설정)

complete linkage (군집 간 element끼리의 거리 중 max를 군집 간 거리로 설정)

average linkage (군집 간 element끼리의 모든 거리를 average)

centroid (군집의 centroid끼리의 거리)

ward (두 군집 간 제곱합 - (군집 내 제곱합의 합))

총 5가지이다.

이제 Dendrogram 을 사용한 계층적 군집화를 해보자.

from scipy.cluster.hierarchy import linkage, dendrogram

scipy 패키지 안에 있는 hierarchy 를 사용한다.

linkage_list = ['single', 'complete', 'average', 'centroid', 'ward']
data = [mall_df, mall_scaled_df]

fig, axes = plt.subplots(nrows=len(linkage_list), ncols=2, figsize=(16, 35))
for i in range(len(linkage_list)):
    for j in range(len(data)):
        hierarchical_single = linkage(data[j], method=linkage_list[i])
        dn = dendrogram(hierarchical_single, ax=axes[i][j])
        axes[i][j].title.set_text(linkage_list[i])
plt.show()

왼쪽 데이터는 스케일링 하지 않은 데이터, 오른쪽은 스케일링을 해준 데이터를 보여준다.

순서대로 single linkage, Complete linkage, average linkage, Centroid linkage, Ward linkage 를 적용했다.

거리를 기준으로 해서 proximity matrix 를 만들고, 이에 따라서 cluster 를 키워나가는데

군집 간 거리를 측정하는 방식이 달라지니 군집화가 이루어진 결과도 확연하게 차이가 나는 것이 보인다.

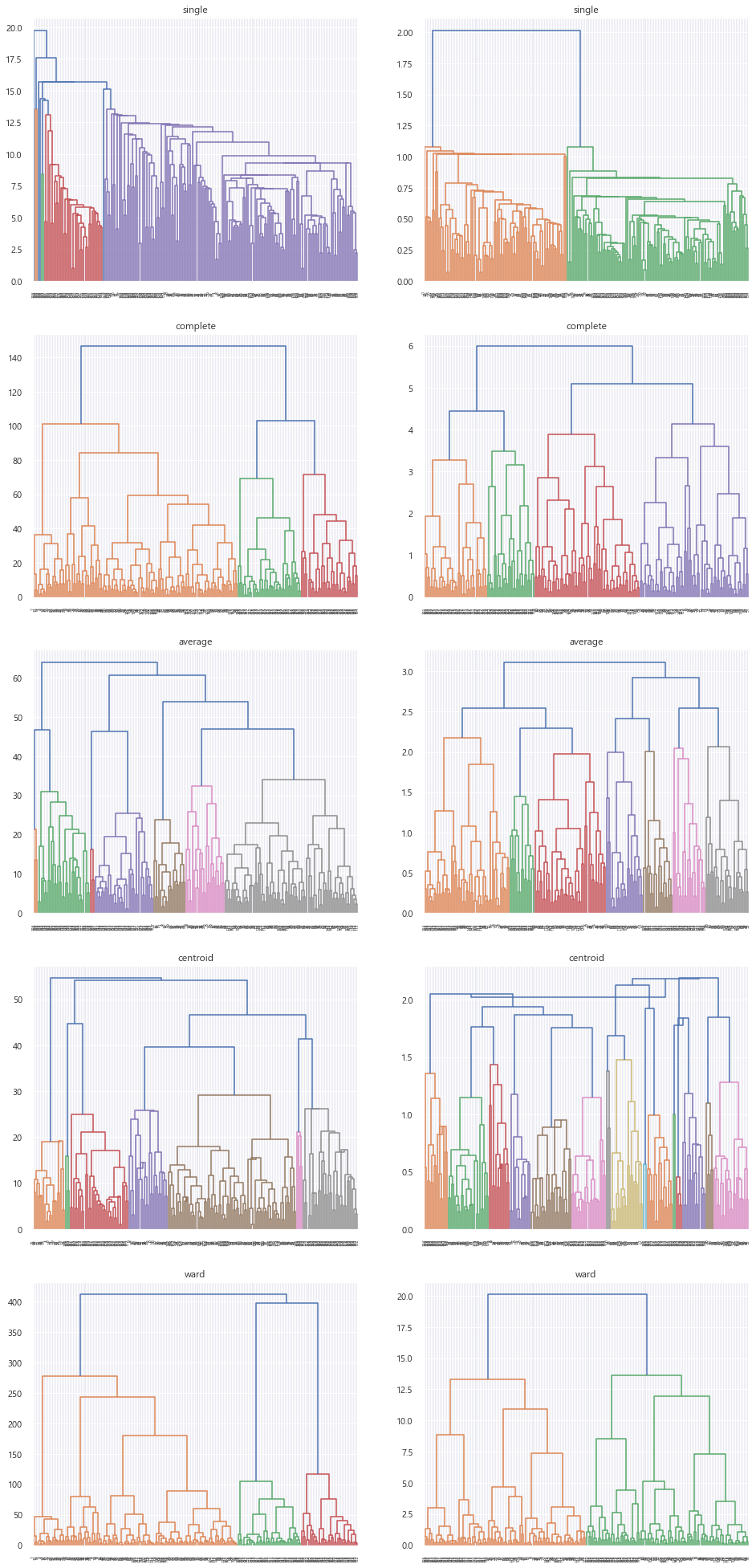
Dendrogram 의 마지막 맨 아래 친구들은 모두 다 데이터 포인트들이다.

트리 위로 올라가면서 가장 가까운 데이터 포인트들끼리 합쳐져서 가지를 만든다.

더 위로 올라가면 가지들끼리 만나서 합쳐진다.

가까운 데이터일수록 아래부분에서 빠르게 합쳐지고, 위에서 합쳐질수록 데이터가 멀다는 뜻이다.

이를 통해서 몇 개의 군집이 적절한 지 선택할 수 있다.

위의 Dendrogram 을 살펴보았을 때,

Average 가 가장 군집이 잘 보이는 것 같다.

그러므로 Cluster = 5 로 해서 군집화를 진행해보겠다.

from sklearn.cluster import AgglomerativeClustering
agg_clustering = AgglomerativeClustering(n_clusters=5, linkage='average')
labels = agg_clustering.fit_predict(mall_df)

scaling하기 전의 데이터(mall_df)로

hierarchical clustering(method='average', n_cluster=5) 를 진행시켰다.

plt.figure(figsize=(20, 6))
plt.subplot(131)
sns.scatterplot(x='Annual Income (k$)', y='Spending Score (1-100)', data=mall_df, hue=labels, palette='Set2')

plt.subplot(132)
sns.scatterplot(x='Age', y='Spending Score (1-100)', data=mall_df, hue=labels, palette='Set2')

plt.subplot(133)
sns.scatterplot(x='Age', y='Annual Income (k$)', data=mall_df, hue=labels, palette='Set2')

어느정도 군집화가 잘 진행된 것 같다.

앞에서 보았던 대로 소비 지수(Spending Score)와 평균 소득(Annual Income) 간의 군집이 보인다.

위의 clustering 결과를 3차원 시각화해보자.

from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d') 

x = mall_df['Annual Income (k$)']
y = mall_df['Spending Score (1-100)']
z = mall_df['Age']
ax.scatter(x, y, z, c = labels, s= 20, alpha=0.5, cmap='rainbow')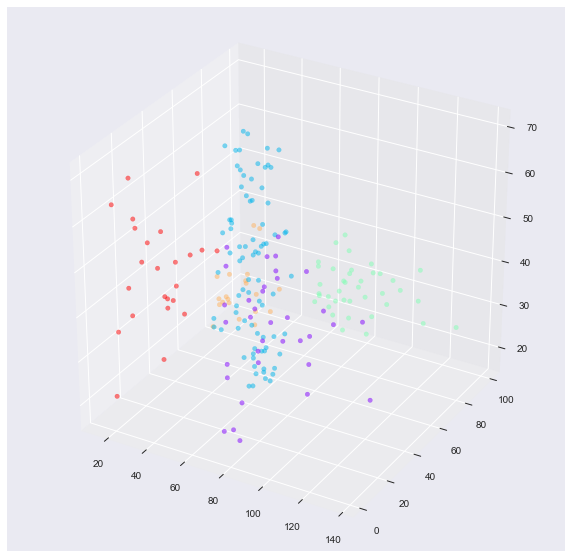

이번에는 Scaling 했을 때의 데이터로 계층적 군집화를 진행해보자.

Ward 방법으로 Scaling 데이터를 Dendrogram 으로 보았을 때 비교적 균등하게 성장하는 것이 보여서

한 번 해보기로 했다.

agg_clustering = AgglomerativeClustering(n_clusters=5, linkage='ward')
labels = agg_clustering.fit_predict(mall_scaled_df)

plt.figure(figsize=(20, 6))
plt.subplot(131)
sns.scatterplot(x='Annual Income (k$)', y='Spending Score (1-100)', 
						data=mall_scaled_df, hue=labels, palette='Set2')

plt.subplot(132)
sns.scatterplot(x='Age', y='Spending Score (1-100)', 
					data=mall_scaled_df, hue=labels, palette='Set2')

plt.subplot(133)
sns.scatterplot(x='Age', y='Annual Income (k$)', data=mall_scaled_df, 
								hue=labels, palette='Set2')

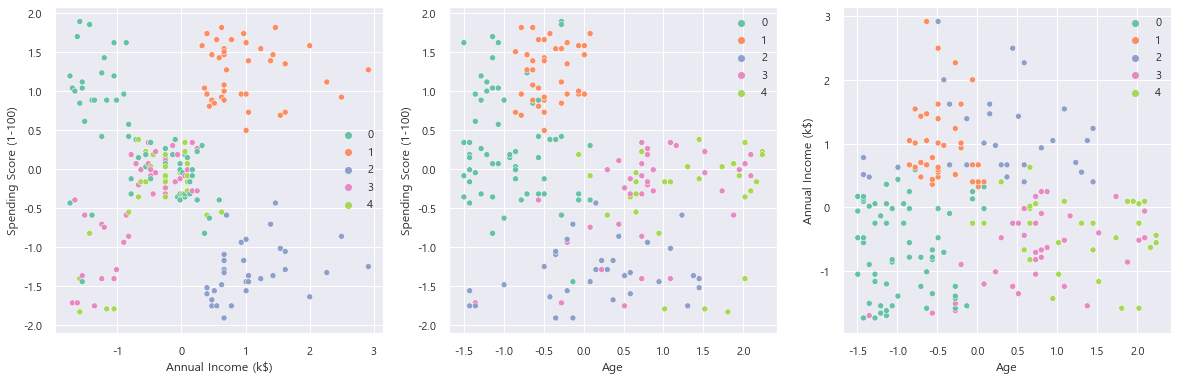
딱히 앞보다 결과가 더 나은 것 같지는 않다.

fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d') 

x = mall_scaled_df['Annual Income (k$)']
y = mall_scaled_df['Spending Score (1-100)']
z = mall_scaled_df['Age']
ax.scatter(x, y, z, c = labels, s= 20, alpha=0.5, cmap='rainbow')

K-means 군집화 ( K-means Clustering )

이전에도 했던 K-means 클러스터링 !

k-means 는 비계층적 군집화 방법들 중, 거리 기반 알고리즘에 속한다.

k-means 는 k개의 init centroid(중심점) 를 설정해두고, 각각의 데이터를 가까운 centroid cluster 로 할당 후에

cluster 내 centroid 를 다시 또 업데이트하고, 다시 각각의 데이터를 가까운 centroid cluster 로

할당하는 과정을 반복한다.

이 과정을 중심점이 변하지 않을 때까지 수행하게 된다.

K-means 에서 중요한 변수는 군집의 개수인 K와 init centroid 이다.

처음의 중심(init Centroid)이 어디인지에 따라서 최종 수렴된 Clustering 결과가 달라질 수

있기 때문에 일부 데이터를 샘플링해서 계층적 군집화(Hierarchical Clustering, 위에서 한 거) 를

진행한 후, 이에 기반해서 최초 중심지점을 지정하기도 한다.

scikit learn 의 K-Means 'k-means++' 방법으로 초기의 중심을 결정하는데,

이 방법은 k개의 초기 centroid 를 결정할 때 중심점1 을 하나 지정하고, 그 다음 중심점2는 이전의

중심점1과는 멀리 떨어지게 잡는 것이다.

또한 군집의 수인 K 는 x축을 k, y축을 군집 내 거리 제곱합의합으로 두고 급격하게 꺾이는 Elbow point를 찾는다.

Elbow point 를 찾는 이유는 군집의 수를 늘렸음에도 불구하고 거리 제곱합이 크게 줄어들지 않는 지점을

찾고자 하는 의도이다.

from sklearn.cluster import KMeans

def change_n_clusters(n_clusters, data):
    sum_of_squared_distance = []
    for n_cluster in n_clusters:
        kmeans = KMeans(n_clusters=n_cluster)
        kmeans.fit(mall_df)
        sum_of_squared_distance.append(kmeans.inertia_)
        
    plt.figure(1 , figsize = (12, 6))
    plt.plot(n_clusters , sum_of_squared_distance , 'o')
    plt.plot(n_clusters , sum_of_squared_distance , '-' , alpha = 0.5)
    plt.xlabel('Number of Clusters')
    plt.ylabel('Inertia')

k에 따라서 inertia_ (군집 내 거리제곱합의 합)이 어떻게 변하는 지 시각화해보자.

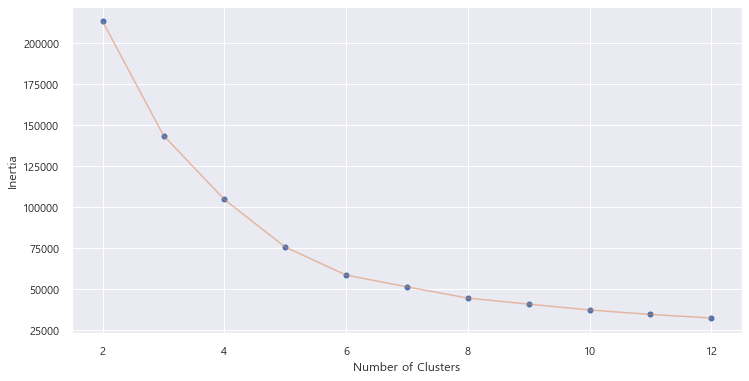
스케일링 하지 않은 mall_df 데이터를 넣었을 때,

군집은 6 정도가 적절한 것 같다.

이제 k-means 의 k값을 6으로 해서 군집화를 시켜보자.

kmeans = KMeans(n_clusters=6)
kmeans.fit(mall_df)

plt.figure(figsize=(20, 6))
plt.subplot(131)
sns.scatterplot(x='Annual Income (k$)', y='Spending Score (1-100)', data=mall_df, hue=kmeans.labels_,palette='coolwarm')
plt.scatter(kmeans.cluster_centers_[:, 2], kmeans.cluster_centers_[:, 3], c='red', alpha=0.5, s=150)

plt.subplot(132)
sns.scatterplot(x='Age', y='Spending Score (1-100)', data=mall_df, hue=kmeans.labels_, palette='coolwarm')
plt.scatter(kmeans.cluster_centers_[:, 1], kmeans.cluster_centers_[:, 3], c='red', alpha=0.5, s=150)

plt.subplot(133)
sns.scatterplot(x='Age', y='Annual Income (k$)', data=mall_df, hue=kmeans.labels_, palette='coolwarm')
plt.scatter(kmeans.cluster_centers_[:, 1], kmeans.cluster_centers_[:, 2], c='red', alpha=0.5, s=150)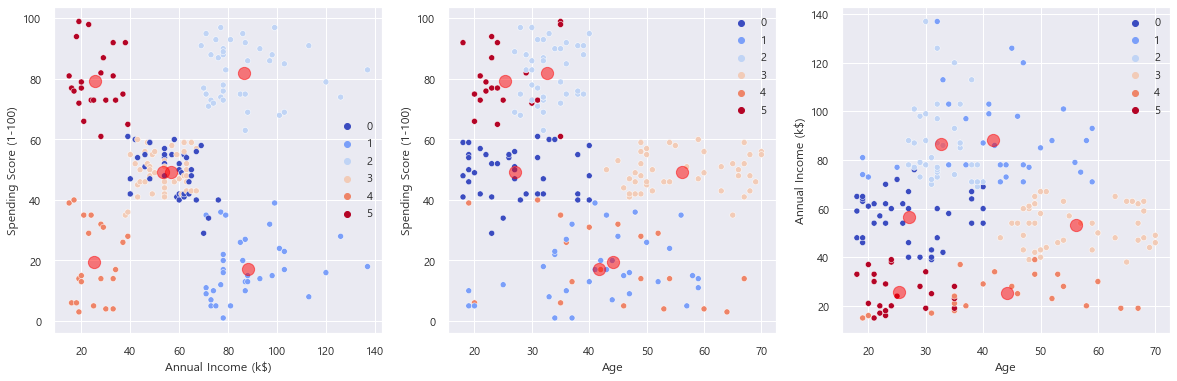

개인적으로는 5가 더 좋을 것 같다.

kmeans = KMeans(n_clusters=5)
kmeans.fit(mall_df)

plt.figure(figsize=(20, 6))
plt.subplot(131)
sns.scatterplot(x='Annual Income (k$)', y='Spending Score (1-100)', data=mall_df, hue=kmeans.labels_,palette='coolwarm')
plt.scatter(kmeans.cluster_centers_[:, 2], kmeans.cluster_centers_[:, 3], c='red', alpha=0.5, s=150)

plt.subplot(132)
sns.scatterplot(x='Age', y='Spending Score (1-100)', data=mall_df, hue=kmeans.labels_, palette='coolwarm')
plt.scatter(kmeans.cluster_centers_[:, 1], kmeans.cluster_centers_[:, 3], c='red', alpha=0.5, s=150)

plt.subplot(133)
sns.scatterplot(x='Age', y='Annual Income (k$)', data=mall_df, hue=kmeans.labels_, palette='coolwarm')
plt.scatter(kmeans.cluster_centers_[:, 1], kmeans.cluster_centers_[:, 2], c='red', alpha=0.5, s=150)

Scaling 전의 데이터를 k = 6으로 군집화해보자.

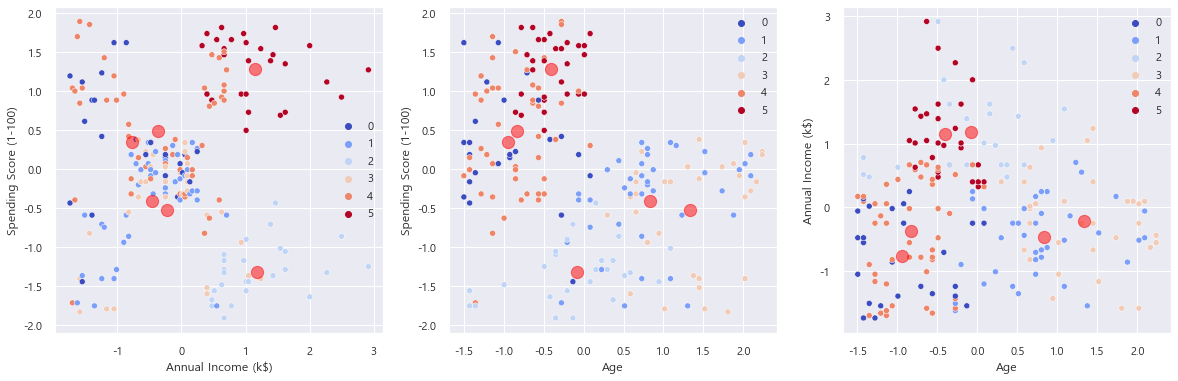
Scaling 후의 데이터보다는 못하지만 어느정도 군집화는 된 것 같다.

나중에 silhouette score로 평가해보도록 하자

참고 :

https://tobigs.gitbook.io/tobigs/data-analysis/undefined-3/python-2-1#1.-preprocessing-eda

클러스터링 실습 (1) (EDA,Sklearn) - Tobigs

n_clusters = [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]

tobigs.gitbook.io

잘 몰라서 배우는 마음으로 그냥 그대로 실습했습니다 ^^..

이론보다 이렇게 직접 실습하면서 배우는 게 머리에 더 잘 남는 것 같다.

항상 이런 어려운 것들 예제랑 실습으로 보여주시는 분들 감사합니다 ㅠ

제 공부에 많은 도움이 돼요 ..