| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- DeepLearning
- k-means
- 빅데이터
- 클러스터링
- 2023공공빅데이터청년인재양성후기
- SQL
- 2023공빅데
- decisiontree
- 텍스트마이닝
- DL
- ADSP
- 오버샘플링
- 데이터분석
- ML
- data
- NLP
- datascience
- 공공빅데이터청년인재양성
- textmining
- 머신러닝
- 공빅
- 공공빅데이터청년인턴
- Kaggle
- machinelearning
- 분석변수처리
- ADsP3과목
- 2023공공빅데이터청년인재양성
- 공빅데
- 데이터전처리
- Keras
- Today
- Total
愛林
[Python/DL] 딥 러닝 (Deep Learning) (1) - 퍼셉트론(Perceptron)과 신경망 본문
[Python/DL] 딥 러닝 (Deep Learning) (1) - 퍼셉트론(Perceptron)과 신경망
愛林 2023. 1. 10. 10:46Deep Learning

ANN 글을 적으면서 간결하게 공부했으나, 처음 보는 개념이라 헷갈리기도 했고
아직 능숙하게 사용하기에는 심층적인 공부가 더 필요할 것 같다는 생각이 들었다.
그래서 정리하는 글
딥 러닝에 대해서 알아보고, keras 를 통해 간결한 사용방법을 익혀보자.
Deep Learning ?
Deep Learning 은 머신 러닝(Machine Learning)의 한 분야로서,
인공 신경망(ANN)의 층을 연속적으로 깊게 쌓아올려 데이터를 학습하는 방식을 말한다.
ANN 에 대한 개념은 앞서 공부했지만, 너무 간결하기도 했고 자격증 공부를 위한 얕은 공부였다.
그래서 이번에도 다시 Perceptron의 개념부터 차근차근 쌓아올려 보기로 했다.
Perceptron
퍼셉트론은 제일 초기 형태의 인공 신경망으로, 다수의 입력에서 하나의 결과를 내보내는 알고리즘이다.
퍼셉트론은 인간 뇌를 구성하는 뉴런과 유사하고, 이를 본따 만들었기에 동작이 유사하다.
뉴런은 여러 갈래의 가지 돌기에서 여러 신호를 받고, 이 신호가 일정치 이상의 크기를 넘어서면
축삭돌기를 통해서 신호를 전달한다.


위는 인간의 뉴런, 그리고 아래는 인공신경망인 퍼셉트론을 그려놓은 것이다.
실제 신경 세포인 뉴런의 축삭돌기 역할을 퍼셉트론에서는 가중치가 대신한다. 각각의 인공 뉴런에서 보내진
입력값은 각각의 가중치와 함께 퍼셉트론(인공뉴런) 에 전달된다.
각각의 입력에 대한 가중치의 값은 클수록 해당 입력값의 비중이 크다는 것을 의미하고,
이는 또한 그 입력값이 중요하다는 것을 의미한다.
뉴런에서는 그 입력과 가중치의 곱의 값이 전달되는데, 여기서 그 값의 전체 합이 임계치(threshold) 를 넘으면
출력신호로 1을 전달하고, 그렇지 않을 경우에는 0을 전달한다.
이렇게 입출력을 결정하는 함수를 활성화함수(Activation Function) 이라고 하며,
대표적으로 우리는 계단함수(Step Function) 를 예로 들 수 있다, 보통 이렇게 생겼다.

이 때 이 계단 함수에 사용된 임계치값을 수식으로 표현할 때는 보통 세타Θ 로 표현한다.
식으로 표현하면 다음과 같다.

위의 식에서 임계치 Θ 를 좌변으로 넘기고 편향 b(bias) 로 표현할 수도 있다.
편향 또한 퍼셉트론의 입력으로 사용된다.
보통 그림으로 표현할 때는 입력값이 1로 고정되고 편향 b가 곱해지는 변수가 된다.


위의 식에서 편향(b) 를 추가해주었다.
보통은 가중치만이 딥러닝에서 찾아야할 변수라고 생각하지만, 이 편향 b 또한 출력값에 영향을 주기 때문에
딥 러닝에서 최적의 값을 찾아야할 변수 중 하나이다.
활성화함수는 초기 인공신경망에서는 계단 함수가 사용됐지만, 지금은 많은 다양한 활성화함수들이 있다.
Sigmoid, Softmax, ReLu 등이 대표적인 예이다.
여기서 활성화 함수를 로지스틱 회귀에서 사용되는 시그모이드 함수를 사용하면,
로지스틱 회귀 모델이 하나의 인공 신경망이 되는 것과 같다.
위와 같이 단일로, 입출력층 하나씩으로 구성된 퍼셉트론을 단층 퍼셉트론(Single-Layer-Perceptron) 이라고 한다.
단층 퍼셉트론은 입력층(input layer) 와 출력층(output layer) 두 개로 구성된다.

단층 퍼셉트론은 층이 하나씩으로만 구성되어 있기 때문에 비선형적으로 분리되는 데이터에 대해서는
제대로 학습이 불가능하다는 한계가 있다.
AND 게이트, NAND 게이트, OR 게이트는 구현이 가능하나, XOR 게이트는 구분할 수 없다.
이 게이트들에 대한 설명은 꽤나 길어지고 복잡할 것 같으므로 생략하고, 비선형적인 데이터에 대한 구분이 어렵다고만
기억해두고 가도록 하자.
다층 퍼셉트론 (MultiLayer Perceptron, MLP)
위에서 말한 비선형적인 데이터는 층을 더 쌓으면 만들 수 있다.
입력층과 출력층 중간에 층을 하나 더 쌓는 것이다. 이렇게 중간에 쌓는 층을 은닉층(Hidden Layer) 라고 한다.
다층 퍼셉트론과 단층 퍼셉트론의 차이는 은닉층의 유무라고 말할 수 있겠다.
단층 퍼셉트론은 입력층, 출력층으로만 이루어진 것이고,
다층 퍼셉트론은 입력층, 은닉층, 출력층으로 이루어진 것이다.
여기서 은닉층이 2개 이상이 되면 심층 신경망(Deep Neural Network, DNN) 이라고 한다.

이전에는 퍼셉트론이 제대로 된 정답을 출력할 때까지 만드는 사람이 직접 가중치를 바꾸어보며 적당한 가중치를 찾았다.
그렇지만 이젠 은닉층이 여러개가 생기며 기계가 가중치를 스스로 찾아낼 수 있게 되었다.
이것이 바로 훈련 (Training) 단계이다.
이러한 훈련은 손실 함수(Loss Function) 과 옵티마이저(Optimizer) 를 사용한다.
이러한 학습을 시키는 대상이 심층신경망인 경우, 이를 우리는 딥 러닝(Deep Learning) 이라고 부른다.
피드 포워드 신경망 (Feed-Forward Neural Network, FFNN)
다층 퍼셉트론(MLP) 에서 입력층에서 오직 출력층 방향으로만 전개되는 신경망을
피드 포워드 신경망(Feed-Forward Neural Network) 라고 부른다.


두 번째 이미지는 순환 신경망(Recurrent Neural Network) 로,
은닉층의 출력값을 출력값으로도 값을 보내나, 은닉층의 출력값이 다시 은닉층의 입력값으로 다시 사용되는 신경망이다.
전결합층 (Dense Layer, Fully-Connected Layer)
다층 퍼셉트론은 은닉층, 출력층의 모든 뉴런이 바로 이전의 뉴런들과 연결되어 있다.
이와 같이 전체가 결합되어 있는 층을 전결합층이라고 하며, Dense Layer 라고 한다.
keras 에서 밀집층을 쌓을 때 Dense 를 이용하며, 아마 가장 많이 볼 함수라고 생각된다.

활성화 함수 (Activation Function)
활성화함수는 뉴런이 전위가 일정한 임계치를 넘어섰을 때 출력을 하는 것과 같은 역할을 해준다.
입력값과 가중치의 곱의 합 , 그리고 여기에 편향(b) 까지 더해진 값을 활성화 함수에 넣었을 때,
일정한 임계치(Threshold) 를 넘어서면 1을 출력한다.
계단함수의 특징은 선형 함수가 아닌 비선형 함수여야 한다는 점이다.
선형 함수란, 출력이 입력의 상수배만큼 변하는 함수를 말한다. y = ax + b 가 전형적인 선형함수이다.
반면 비선형함수란, 직선 1개로는 그릴 수 없는 함수를 말한다.
인공 신경망에서 사용되는 계단함수 또한 비선형 함수이다.
인공 신경망의 성능을 올리기 위해서는 은닉층을 적절하게 추가해야 한다.
그러나 만약 활성화 함수로 선형함수를 사용하게 되면 은닉층을 쌓는 것이 소용이 없어진다.
예를 들어서 활성화 함수가 f(x) = wx 일 때, 동일한 활성화 함수를 사용하는 은닉층을 2개 쌓는다고 하면
출력층을 포함하여 y(x) = f(f(f(x))) 가 된다. 이를 식으로 표현하면 w*w*w*x 가 된다.
이 식은 사실상 w^3 을 w라고 정의하게 된다면, 그냥 y(x) = w^3x = kx 같은 형태가 된다.
그냥 선형함수의 기울기가 제곱인거나 다름이 없다. 은닉층이 소용이 없는 것이다.
그렇지만 아예 선형 함수를 활성화함수로 사용하지 않는 것도 아니다.
종종 활성화 함수를 사용하지 않는 층을 비선형 층들왁 함께 인공 신경망의 일부로서 추가하는 경우도 있다.
그 예시로는 Embedding Layer 가 있다.
활성화 함수의 예로 앞서서는 계단 함수 (Step Function) 을 살펴보았으나, 실제로는 더 많은 활성화 함수가 있다.
이를 몇 가지만 알아보자.
1) 계단함수 (Step Function)
제일 처음 사용했던 활성화 함수로, 실제로는 잘 쓰이지 않지만 보통 인공신경망을 처음 배울 때 접한다.

2) 시그모이드 함수 (Signoid Function)
Step Function 을 살펴보면 도중에 한번 끊겼다가 1로 가게 된다.
이는 미분연산을 불가능하게 만들기 때문에 시그모이드 함수가 등장했다.
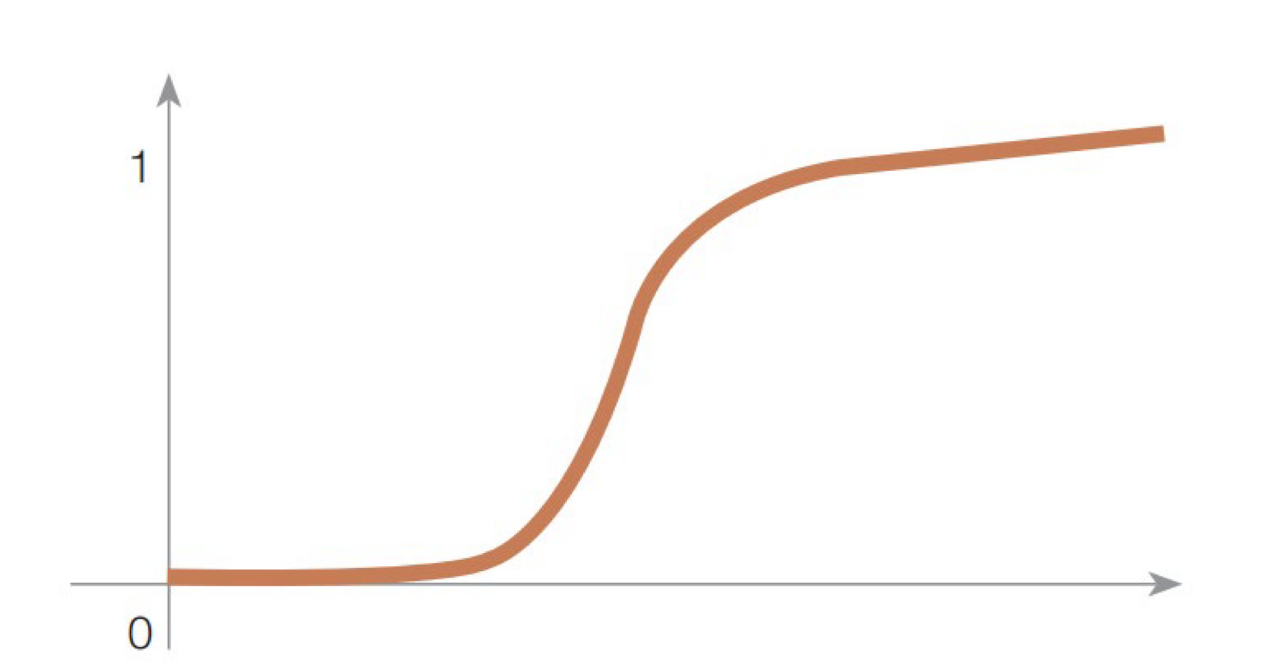
tanh (Hyperblic tangent) 를 활용하기도 한다.

3) 기울기 소실 (Vanishing Gradient)
인공신경망은 입력층에서 출력층으로 가는 순전파(Forward propagation) 연산을 하고,
이후 그 순전파 연산을 통해 나온 예측값과 실제값의 오차를 손실 함수(Loss Function) 을 통해 계산한다.
그리고 이 손실을 미분을 통해 기울기(Gradient) 를 구하고, 출력층에서 입력층 방향으로 가중치와 편향을 업데이트 하는 과정인 역전파(Back Propagation) 을 수행한다. 이 역전파를 하는 과정에서 인공신경망은 경사 하강법을 사용하는데,
이 과정에서 위와 같이 말했듯이 미분이 수행된다.
위와 같은 함수들의 문제점은 앞뒤로 기울기가 0에 가깝다는 것이다.
0과 1에 가까워질수록 그래프가 완만해지고, 기울기는 0에 가깝게 된다.

또한 초록색 구간에서도 미분값이 최대가 0.25이다. (Sigmoid Function 기준)
이렇게 작은 미분값으로 계속 역전파 연산을 계속한다면, 0에 가까운 값이 곱해지기 때문에 앞쪽으로 갈수록
미분값 (기울기, Gradient) 가 잘 전달되지 않게 된다.
이를 기울기가 앞으로 갈수록 서서히 소멸한다는 뜻에서 기울기 소실 문제 (Vanishing Gradient) 라고 한다.

아무튼간, 이러한 이유로 시그모이드 함수나 tanh 함수는 은닉층에서 잘 사용되지 않는다.
시그모이드 함수는 보통 이진 분류를 위해 출력층에서 많이 사용하게 된다.
4) 렐루 함수 (ReLU Function)
인공신경망의 은닉층에서는 가장 핫한 함수라고 볼 수 있다.

렐루 함수는 음수를 입력하면 0을 출력하고, 양수를 입력하면 입력값을 그대로 반환하는 것이 특징이다.
그러므로 출력값이 특정 양수값에 수렴하지 않는다. 0 이상의 입력값의 경우에는 미분값이 항상 1이다.
깊은 신경망의 은닉층에서 시그모이드 함수보다 훨씬 더 잘 작동한다.
뿐만 아니라 렐루 함수는 시그모이드와 같이 어떤 연산이 필요한 것이 아니라 단순 임계값이기 때문에
연산속도도 빠르다.
하지만 치명적인 단점으로, 입력값이 음수가 등장하면 기울기 또한 0이 된다.
기울기가 0인 뉴런은 다시 회생하는 것이 매우 어렵다. 우리는 이걸 죽은 렐루(Dying ReLU)라고 한다.
그러나 위와 같이 죽은 렐루 문제를 해결하기 위해 ReLU의 변형으로 등장한 함수들은 많다.
Leaky ReLU, ELU, Parameter ReLU, SELU, google의 Swish, Maxout 등이 있다.
5) 리키 렐루 (Leaky ReLU)
리키 렐루는 음수를 0.01배 해주므로 입력값이 음수일 지라도 0이 아닌 0에 가까운 매우 작은 수를 반환하도록 되어있다.
하이퍼파라미터로 leaky (새는) 정도를 결정하며 일반적으로는 0.01 의 값을 가진다.
여기서의 leaky 정도는 입력값이 음수일 때의 기울기를 비유한다.
그러나 leaky 함수 또한 음수에서 선형성이 생기게 되고, 그로 인해 위에서 말했던 문제들이 발생하여
복잡한 분류에서는 사용할 수 없다는 특징이 있다.
일부 사례에서는 오히려 Sigmoid나 tanh보다도 성능이 떨어진다는 얘기 또한 나온다.
그러나 만일 음수가 매우 중요하다면 제한적으로 사용하는 것이 추천된다.

6) ELU (Exponential Linear Unit)
E렐루는 2015년에 나온 비교적 최근에 나온 함수로, 각져있는 형태인 ReLU 를 exp 를 사용하여
부드럽게 만든 렐루함수이다.

ELU는 ReLU 보다 부드러운 형태를 지니고 있으므로, 미분 시에 0에서 끊어지는 렐루와 달리
미분해도 부드럽게 기울기가 이어진다.
ELU 는 그러므로 ReLU의 대표적인 대안 방법 중에 하나가 된다.
ELU 는 리키 렐루와는 다르게 음에서도 비선형적인 형태를 지니고 있어 복잡한 분류에서도 사용이 가능하다.
경사 하강법에서 수렴 속도 또한 빠르다.
그러나 ReLU에 비해서 성능이 크게 증가한다는 이슈가 없고, 오히려 exp로 인해 연산이 오래걸려 학습속도가
ReLU보다 늦어지기에 잘 사용하지 않는다. 오히려 소모되는 시간보다 성능 향상이 미비하거나 성능이 내려가기도
한다는 말이 있다.
7) 소프트맥스 함수 (Softmax Function)
은닉층에서는 보통 ReLU 를 사용하는 것이 매우 일반적이다.
시그모이드와 같이 출력층에서 많이 사용되는 함수가 바로 소프트맥스 함수이다.
시그모이드 함수가 이진분류(Binary Classification) 에서 사용된다면, 소프트맥스 함수는 세 가지 이상의 클래스가 있는
다중 클래스 분류(MaltiClass Classification) 문제에서 주로 사용된다.
각 클래스에 속할 확률을 구해주는 함수이다.
Softmax 함수의 가장 큰 장점은 확률의 총합이 1이기 때문에, 어떤 분류에 속할 확률이 가장 높을 지를 쉽게 인지할 수 있다.

정리하자면,
딥러닝으로 이진 분류를 할 때에는 출력층에 앞서서 배운 시그모이드를 사용하고(Logistic Regrssion),
딥 러닝으로 다중 클래스 분류 문제를 풀 때는 출력층에 소프트맥스를 보통 사용한다.
순전파 (Foward Propagation)

입력층이 은닉층을 지나 출력층까지 단방향으로 , 앞으로만 전진하는 연산을 순전파(Foward Propagation) 이라고 한다.
입력값은 각 층을 지날 때 가중치와 함께 연산되어 출력층으로 나아간다. 출력층에서는 모든 연산이 끝난 결과를 출력한다.
이를 행렬로 구현해보자.

위와 같은 완전 연결 신경망 (Dense) 이 있다.
입력 차원이 3, 출력 차원이 2인 저 인공신경망을 Python 을 통해 구현해본다면,
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
model = Sequential()
# 3개의 입력과 2개의 출력
model.add(Dense(2, input_dim = 3, activation = 'softmax'))활성화함수는 SoftMax 를 사용했다.
이진분류 문제이지만 소프트맥스는 이진 분류 또한 수행이 가능하다.
- tensorflow keras 2.9.0 version
- Python 3.9.12
keras 에서는 summary() 를 통해 이 모델에 존재하는 모든 가중치 w 와 편향 b를 확인할 수 있다.
model.summary()Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 2) 8
=================================================================
Total params: 8
Trainable params: 8
Non-trainable params: 0
_________________________________________________________________총 파라미터는 8개이다.
위 신경망에서 학습가능한 매개변수인 w와 b의 개수가 총 합해서 8개라는 의미이다.
위를 행렬의 곱 관점에서 이해한다면,

입력층의 뉴런이 3개, 출력층의 뉴런이 2개이다.
화살표 각각은 가중치 w 를 가지고 있다. 위에서 총 화살표의 개수는 6개이므로, 가중치 w 또한 6개이다.
이를 행렬곱 관점에서는 3 x 2 행렬연산을 했다고 볼 수 있다. 3차원 벡터를 2차원으로 만들기 위한 연산이다.
이 행렬의 원소는 각 가중치 w 이다.
일반적으로 편향 b는 생략되는 경우가 많지만 위에서는 b1, b2로 각각 식에 넣어주었다.
가중치의 개수는 6개, 편향의 개수는 2개이므로, 학습가능한 총 매개변수 수는 summary() 에서 보았듯이
8개가 맞다.
y1과 y2 를 구하는 과정을 수식으로 표현한다면,

좀 더 간단하게 식을 표현해보자면,
Y = XW + B 로 표현이 가능하다.

조금 더 복잡하게 병렬 연산을 구현해보자.
인공 신경망이 4개의 샘플을 동시에 처리해본다고 가정하자.
4개의 샘플을 하나의 행렬 X 에 넣고 인공신경망의 순전파를 행렬곱으로 표현하면 다음과 같다.

여기서 혼동하지 말아야 하는 것은 우리는 인공신경망의 4개의 샘플을 동시에 처리하고 있지만,
매개변수는 여전히 8개라는 점이다. 이렇게 여러개의 샘플을 동시에 처리하는 것을 우리는 '배치 연산' 이라고 한다.
은닉층을 추가하여 조금 더 깊은 신경망을 만들어보자.

위와 같은 신경망을 keras 로 구현해본다면 다음과 같다.
4개의 입력, 2개의 은닉층에 8개, 다시 3개의 출력이다.
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
model = Sequential()
# 4개의 입력과 8개의 출력
model.add(Dense(8, input_dim = 4, activation = 'relu'))
# 이어서 8개의 출력
model.add(Dense(8, activation = 'relu'))
# 이어서 3개의 출력
model.add(Dense(3, activation = 'softmax'))활성화함수는 relu와 출력층에는 softmax를 사용했다.
각 층을 기준으로 입출력의 개수를 정리하면 다음과 같다.
- 입력층 : 4개의 입력과 8개의 출력
- 은닉층1 : 입력층에서 출력받은 8개의 입력과 8개의 출력
- 은닉층2 : 은닉층1에서 출력받은 8개의 입력과 3개의 출력
- 출력층 : 은닉층2에서 출력받은 3개의 입력과 3개의 출력 (Softmax 연산 수행)
행렬연산은 위와 동일하게 하면 된다.
입력층만 보았을 때, 입력행렬은 1x4 의 행렬, 출력은 8개이므로 출력행렬은 1x8의 행렬.
중간의 편향 행렬은 출력 행렬과 동일하므로 1x8의 행렬,
중간의 가중치 행렬 (w) 는 입력행렬을 출력행렬과 동일하게 만들어주어야 하므로 4x8의 행렬을 가지게 된다.
입력층과 은닉층1의 층1개만 식으로 표현해보았다.


Review
활성화 함수를 더 다양하게 공부해보고 싶다는 생각이 들었다.
진행하고 있는 이중분류 프로젝트에서 Sigmoid 를 이용하여 신경망을 쌓아봐야겠다는 생각이 들었다.
Dense 를 쌓을 때 기초지식이 없어서 파라미터에 무슨 숫자를 넣어야 할 지 좀 헷갈렸는데 이제는
감이 좀 잡히는 것 같다.
참고
07-01 퍼셉트론(Perceptron)
인공 신경망은 수많은 머신 러닝 방법 중 하나입니다. 하지만 최근 인공 신경망을 복잡하게 쌓아 올린 딥 러닝이 다른 머신 러닝 방법들을 뛰어넘는 성능을 보여주는 사례가 늘면서, …
wikidocs.net
https://wndofla123.tistory.com/84
[Python/DL] 분류 알고리즘 (Classification Algorithm) : 인공신경망 (ANN : Article Neural Network)
2022.12.07 + 교육 내용 추가 인공신경망 (Article Neural Network : ANN) 인공신경망이란, 인간 뇌를 기반으로 한 추론 모델이다. 뉴런을 기본적인 정보처리 단위로 하여 만든 시스템이다. 인간의 뇌는 100억
wndofla123.tistory.com
딥러닝-3.5. 활성화함수(6)-ReLU Family
앞서 은닉층에서 자주 사용되는 함수인 렐루(ReLU)에 대해 알아보았다. 그러나, 렐루 함수는 음수인 값들을 모두 0으로 만들어 Dying ReLU를 만드는 문제점이 있다고 하였다. 렐루 함수는 아주 단순
gooopy.tistory.com
https://ml-cheatsheet.readthedocs.io/en/latest/activation_functions.html
Activation Functions — ML Glossary documentation
Exponential Linear Unit or its widely known name ELU is a function that tend to converge cost to zero faster and produce more accurate results. Different to other activation functions, ELU has a extra alpha constant which should be positive number. ELU is
ml-cheatsheet.readthedocs.io




