| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 공공빅데이터청년인재양성
- machinelearning
- DeepLearning
- Keras
- 공빅
- 2023공공빅데이터청년인재양성후기
- NLP
- 오버샘플링
- ADsP3과목
- 공빅데
- Kaggle
- ADSP
- decisiontree
- 분석변수처리
- k-means
- ML
- 빅데이터
- DL
- 데이터전처리
- 머신러닝
- SQL
- 2023공공빅데이터청년인재양성
- data
- 2023공빅데
- datascience
- textmining
- 데이터분석
- 텍스트마이닝
- 공공빅데이터청년인턴
- 클러스터링
- Today
- Total
愛林
[Python/Data] Load_diabetes 데이터셋을 이용한 회귀분석 실습 - 단순선형회귀분석 (Simple Regression Analysis) 본문
[Python/Data] Load_diabetes 데이터셋을 이용한 회귀분석 실습 - 단순선형회귀분석 (Simple Regression Analysis)
愛林 2022. 7. 21. 00:29

회귀분석 가보자고 ..
회귀분석 (Regression Analysis) 실습
관련 패키지 import + 시각화 준비 (깨지지 않도록 폰트 지정)
import pandas as pd
import warnings
warnings.simplefilter(action = 'ignore', category = FutureWarning)
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
import os
# 깨짐 방지를 위한 Font 지정
import os
if os.name =='nt' :
font_family = "Malgun Gothic"
else :
font_family = "AppleGothic"
# 값이 깨지는 문제 해결을 위해 파라미터값 설정
sns.set(font=font_family, rc = {"axes.unicode_minus" : False})
우리가 사용할 데이터는
skcit learn 의 load_diabetes Data set. 당뇨병 진행도 예측 데이터이다.
from sklearn.datasets import load_diabetes
10종류의 독립변수, 독립변수의 값들은 모두 스케일링.
종속변수는 target 이다.
target : 1년 뒤 측정한 당뇨병의 진행률이다.
독립변수는 age(나이), sex(성별), bmi(비만도지수), bp(평균혈압), s1~s6(6종류의 혈액 검사 수치)
data = load_diabetes()
df = pd.DataFrame(data.data, columns = data.feature_names)
df['target'] = data.target
df.head()
data 에 diabetes 데이터를 저장했다.
age sex bmi bp s1 s2 s3 s4 s5 s6 target
0 0.038076 0.050680 0.061696 0.021872 -0.044223 -0.034821 -0.043401 -0.002592 0.019907 -0.017646 151.0
1 -0.001882 -0.044642 -0.051474 -0.026328 -0.008449 -0.019163 0.074412 -0.039493 -0.068332 -0.092204 75.0
2 0.085299 0.050680 0.044451 -0.005670 -0.045599 -0.034194 -0.032356 -0.002592 0.002861 -0.025930 141.0
3 -0.089063 -0.044642 -0.011595 -0.036656 0.012191 0.024991 -0.036038 0.034309 0.022688 -0.009362 206.0
4 0.005383 -0.044642 -0.036385 0.021872 0.003935 0.015596 0.008142 -0.002592 -0.031988 -0.046641 135.0
이제 이 친구들의 상관계수를 corr() 로 확인해본다.
절대값이 1에 가까울수록 상관도가 높은 것임을 기억하자.

눈에 띄는 상관계수로는 ... bmi 와 target (0.5864, 사실 그렇게 높은 값은 아닌 것 같은데) ,
s1과 s2 (0.896) 정도인 듯 하다.
데이터가 너무 많아서 눈이 침침해진다 ...
아무튼 간에 단순선형회귀분석을 진행해보자.
우리는 BMI 와 Target 으로 분석해볼 것이다.
단순선형회귀분석 실습
먼저 데이터의 정보를 탐색해보자.
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 442 entries, 0 to 441
Data columns (total 11 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 age 442 non-null float64
1 sex 442 non-null float64
2 bmi 442 non-null float64
3 bp 442 non-null float64
4 s1 442 non-null float64
5 s2 442 non-null float64
6 s3 442 non-null float64
7 s4 442 non-null float64
8 s5 442 non-null float64
9 s6 442 non-null float64
10 target 442 non-null float64
dtypes: float64(11)
memory usage: 38.1 KB
산점도도 같이 확인해보자.
sns.regplot('bmi', 'target', lowess = True, line_kws={'color' : 'red'}, data = df)<AxesSubplot:xlabel='bmi', ylabel='target'>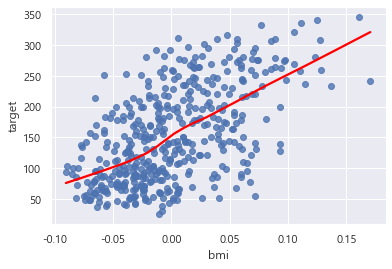
seaborn 패키지의 regplot() 을 사용해서 추세선을 이용한 산점도를 확인해보았다.
lowess = True 는 국소회귀법을 사용해서 추세선을 그리게 된다.
이상값을 확인해보자.
## 이상값 확인
fig , (ax1, ax2) = plt.subplots(1,2)
sns.boxplot('bmi', data = df, ax=ax1)
ax1.set_title('bmi')
# dist 의 상자 그림을 두 번째로 그린다
sns.boxplot('target', data=df, ax=ax2)
ax2.set_title('rate')Text(0.5, 1.0, 'rate')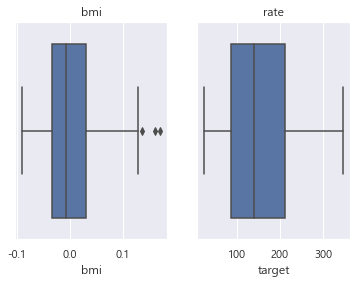
bmi 데이터 쪽에 이상값이 보인다.
분포를 시각화해보자.
## 분포 시각화
fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (10,4))
sns.kdeplot(df['bmi'], ax=ax1)
ax1.set_title('bmi')
sns.kdeplot(df['target'], ax=ax2)
ax2.set_title('rate')Text(0.5, 1.0, 'rate')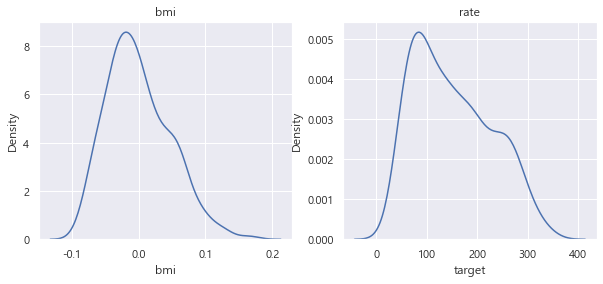
kdeplot을 이용했다. 밀도plot 을 만드는 seaborn 패키지 함수이다.
bmi 와 rate 를 밀도함수로 만들어주었다.
거의 정규분포 비스무리한 것을 확인할 수 있다. (조금 이상하긴 하지만.)
이번에는 비대칭을 확인해보자.
비대칭은 왜도 (Skewness) 로 확인한다.
# 비대칭 확인 (왜도)
import scipy.stats
print(scipy.stats.skew(df['bmi']))
print(scipy.stats.skew(df['target']))0.5961166556214368
0.43906639932477265
scipy.stats 의 skew() 를 사용해서 왜도를 살펴보았다.
왜도 > 0 이므로 살짝 왼쪽으로 치우친 것을 볼 수 있다.
근데 아주 살짝 치우친 것이므로 크게 개의치 않아도 되지 싶다.
sklearn 의 LinearRegression 을 사용해서 회귀분석을 진행해보자.
from sklearn.linear_model import LinearRegression# 데이터셋 생성
X = df.bmi.values
y = df.target.values
l_train_X1 = X.reshape(-1,1)
l_test_y1 = y.reshape(-1,1)
print(X.shape)
print(l_train_X1.shape) # 형태를 바꾸어주었다.데이터를 준비했다.
이제 모델에 데이터를 피팅시켜서 모델을 학습시켜보자.
## 모델 학습
lr_model = LinearRegression()
lr_model.fit(l_train_X1, l_test_y1)
회귀계수 (Coefficient) 를 확인해보자.
이전에, 회귀계수는 Y절편과, 기울기였다. (B0, B1)
print(lr_model.coef_[0]) # 기울기값
print(lr_model.intercept_) # y절편[949.43526038]
[152.13348416]
coef_[0] 는 기울기값,
intercept_ 는 y절편값이다.
이걸 바탕으로 해서 선형회귀 모델로 값을 예측해본다.
lr_model.predict([[-2], [-1], [0], [1], [2]])array([[-1746.73703661],
[ -797.30177622],
[ 152.13348416],
[ 1101.56874455],
[ 2051.00400493]])맞는 지 확인해보자.
lr_model.coef_[0] * -2 + lr_model.intercept_array([-1746.73703661])위랑 똑같은 결과가 나왔다.
잘 학습된 것 같다.
이제 잔차를 계산해보자.
lr_prediction = lr_model.predict(l_train_X1) # lr_prediction 값
lr_residuals = l_test_y1 - lr_prediction # 잔차
잔차는 우리가 test값 - 예상한 값 prediction 값 (선형모델값) 이다.
prediction 값은 X1 train 값을 선형모델에 넣어서 돌린 y값이다.
아무튼간에 식을 작성해주었다.
다음은 R^2. R-squared . 결정계수를 계산해준다.
결정계수는 선형모델에서 아주아주 중요한 값이었다.
전체 분산값 중에 선형모델이 설명하는 값의 비율이었다.
이 결정계수의 값이 0.65 이상이어야 유효했고,
SST - SSR / SST 식을 가지고 있었다.
SST(전체 분산값, 총제곱합), SSR(선형모델이 설명하는 값, 회귀제곱합)
1 - SSE / SST 또한 결정계수의 값이다.
# R_squared 계산
SSE = (lr_residuals **2).sum() # 잔차의 제곱합.
SST = ((l_test_y1 - l_test_y1.mean())**2).sum() # 총변동 혹은 총제곱합
R_squared = 1 - (SSE/SST)
print('R_squared : ', R_squared)
SSE 는 잔차의 제곱합이므로,
아까 위에서 구한 lr_residuals 를 제곱한 값을 모두 sum() 한다.
SST 는 총 제곱합이므로, 데이터 값에서 평균을 빼준 것을 제곱해준다. 그리고 이것도 sum() 해준다.
결정계수는 1- (SSE/SST) 이다.
R_squared : 0.3439237602253802
결정계수가 0.65를 넘지 않으므로, 유효하지 않은 결정계수값이다.
그러므로 BMI 는 Target 을 설명할 수 없다.
그럼 이 모델을 시각화해보자.
sns.regplot(l_train_X1, l_test_y1, lowess=True, line_kws = {'color' : 'red'}, data= df)
plt.title('y = {}*x + {}'.format(lr_model.coef_[0], lr_model.intercept_))
plt.show()

아까 처음에 bmi 랑 Target 이랑 했던 산점도랑 똑같이 나왔다. 당연함. 같은 데이터임..
단순선형회귀 통계적 분석
그럼 이제 단순선형회귀를 통계적으로 분석해보자.
OLS 를 사용해보자,
OLS 는 최소자승법(최소제곱법) 이다. 잔차제곱합을 최소화하는 방법이었다.
OLS 를 불러와주자.
from statsmodels.formula.api import ols
종속변수는 Target, 독립변수는 bmi 를 피팅시켜주자.
res_sr = ols('target ~ bmi', data = df).fit() # 종속변수 = target, 독립변수 = bmi
결과를 확인해보자.
summary() 를 사용하면 결과를 확인할 수 있다.
res_sr.summary()

[ 해석 ]
R-squared 결정계수도 0.344 (아까 구한 거랑 같음)
1에 가까울 수록 좋다.
coef 는 회귀계수 Coefficient 이다.
[949.43526038]
[152.13348416]
위에서 구한 기울기값은 949, Y절편값이 152였다.
Intercept 가 Y절편값이고, bmi 가 기울기값이다.
Target = bmi * 949 + 152
회귀식인 것이다.
No.observations 는 442. 그러니까 442개의 표본수를 가지고 분석을 했다는 말이다.
Df Residuals 는 잔차의 자유도이다.
(잔차의 자유도 : 표본 수 - 종속변수 개수 - 독립변수 개수)
Prob(F-staatistic) 이3.47e -42 로,
0.05보다 작은 값이 나왔다. (유의확률)
유의미하다는 뜻이다.
P>|t| 는 독립변수의 유의확률인데 0.025로 0.05보다 작으므로 유의미하다.
결과 요약
target 에대하여 bmi 로 예측하는 회귀분석을 실시한 결과,
이 회귀모델은 통계적으로 유의미했다.
F(1,440) = 230.7, p<0.05
bmi 독립변수의 회귀계수는 949.4353으로, target 에 대하여 유의미한 예측 변인인 것으로 나타났다.
'Data Science > DATA' 카테고리의 다른 글
| [Python/Data] 탐색적 데이터 분석(EDA) - 다변량 데이터 분석 (2) | 2022.07.24 |
|---|---|
| load_diabetes 데이터셋을 이용한 회귀분석 실습 - 다중선형회귀분석 (Multiple Linear Regression Analysis) (2) | 2022.07.22 |
| [Python/Data] 회귀분석 (Regression Analysis) 설명 (2) | 2022.07.20 |
| [Python/Data] 탐색적 데이터 분석 - 표본추출(단순확률표본추출, 계통표본추출, 층화표본추출) (1) | 2022.07.20 |
| Python으로 배우는 데이터 전처리 이해(II) - 분석변수 처리 - 차원 축소(Dimensionality Reduction) (2) | 2022.07.13 |




