| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 클러스터링
- ML
- 공공빅데이터청년인재양성
- 빅데이터
- 데이터분석
- 공공빅데이터청년인턴
- 데이터전처리
- DeepLearning
- k-means
- machinelearning
- 분석변수처리
- 2023공공빅데이터청년인재양성
- textmining
- Keras
- ADSP
- 공빅
- Kaggle
- ADsP3과목
- SQL
- 2023공공빅데이터청년인재양성후기
- 오버샘플링
- 2023공빅데
- 공빅데
- data
- NLP
- datascience
- decisiontree
- 텍스트마이닝
- DL
- 머신러닝
- Today
- Total
愛林
load_diabetes 데이터셋을 이용한 회귀분석 실습 - 다중선형회귀분석 (Multiple Linear Regression Analysis) 본문
load_diabetes 데이터셋을 이용한 회귀분석 실습 - 다중선형회귀분석 (Multiple Linear Regression Analysis)
愛林 2022. 7. 22. 20:13https://wndofla123.tistory.com/44
load_diabetes 데이터셋을 이용한 회귀분석 실습 - 단순선형회귀분석 (Simple Regression Analysis)
회귀분석 가보자고 .. 회귀분석 (Regression Analysis) 실습 관련 패키지 import + 시각화 준비 (깨지지 않도록 폰트 지정) import pandas as pd import warnings warnings.simplefilter(action = 'ignore', categ..
wndofla123.tistory.com
이전의 단순선형회귀분석과 이어지는 다중선형회귀분석 ..
다중선형회귀 (Multiple Linear Regression)
다중선형회귀는 ,
독립변수가 2개 이상이고 종속변수가 1개인 모델이다.
다중선형회귀분석 실습
import pandas as pd
import warnings
warnings.simplefilter(action = 'ignore', category = FutureWarning)
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
import os
# 깨짐 방지를 위한 Font 지정
import os
if os.name =='nt' :
font_family = "Malgun Gothic"
else :
font_family = "AppleGothic"
# 값이 깨지는 문제 해결을 위해 파라미터값 설정
sns.set(font=font_family, rc = {"axes.unicode_minus" : False})
from sklearn.datasets import load_diabetes
먼저 필요한 패키지를 import 해준다.
print(df.shape)
df.head(3)
df.corr()
을 사용해서 상관계수를 확인해준다.

역시나 이전과 같다.
seaborn 을 사용해서 히트맵을 만들어서 상관계수 데이터를 다시 확인해본다.
cmap = sns.light_palette("red", as_cmap = True)
sns.heatmap(df.corr(), annot=True, cmap = cmap)
plt.show()
빨간색으로 만들었다. annot = True 는 텍스트를 추가하는 것이다.


자 이제 본격적으로 실습 시작.
실습 데이터를 만들어주자.
# 데이터셋 준비
dlr_train_X_df = df.copy()
dlr_train_X_df = dlr_train_X_df.drop("target",1)
dlr_test_y = df.target.values
dlr_test_y = dlr_test_y.reshape(-1,1)
dlr_train_X_df.head()
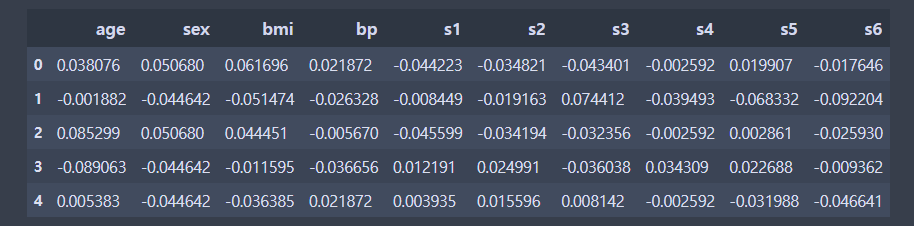
target 컬럼은 지워주었다.
이제 회귀모델을 만들어주자.
dlr_model = LinearRegression()
dlr_model.fit(X = dlr_train_X_df, y= dlr_test_y)
print('절편 : ', dlr_model.intercept_)
print('회귀계수 : ', dlr_model.coef_)절편 : [152.13348416]
회귀계수 : [[ -10.0098663 -239.81564367 519.84592005 324.3846455 -792.17563855
476.73902101 101.04326794 177.06323767 751.27369956 67.62669218]]
dlr_model 이라는 선형회귀모델에 위에서 만든 데이터들을 피팅해주고 ,
단순선형에서도 구했던 것처럼 절편과 회귀계수를 구해본다.
다중회귀이기 때문에, 회귀계수도 여러 개가 나온다.
intercept_ 는 절편을 구해주고 , coef 는 회귀계수, 기울기를 구해준다.
잔차를 구해보자.
prediction = dlr_model.predict(dlr_train_X_df)
residuals = dlr_test_y - predictiony 결과값에 예측한 것을 빼면 잔차가 나온다.

이번에는 R-squared 를 구해주자.
# R_squared 계산
SSE = (residuals ** 2).sum()
SST = ((dlr_test_y - dlr_test_y.mean())**2).sum()
R_squared = 1 - (SSE/SST)
print('R_squared : ', R_squared)
앞서,
R-squared 는 결정계수라고 했다. (너무 안 외워져)
결정계수는 전체분산값 / 예측값 이었다.
1 - SSE/SST = R_squared 이다.
SSE 는 잔차제곱합으로, 앞서 구했던 residuals (잔차) 를 제곱한 것을 모두 더해주면 된다.
이게 전체 분산값
SST 는 실제값에서 우리 예측값이 구한 결과값의 평균을 뺀 분산값을 제곱해서 모두 더해준다.
R_squared : 0.5177484222203499
0.517 정도의 R-squared 가 나왔다.
0.65 이상의 R-squared 가 나오면 유효한것이다.
이제 mse(Mean squared Error : 평균제곱편차, 오차제곱합의 평균) 와
rmse(Root Mean Squared Error : 평균제곱근편차) 를 사용해서 우리가 만든 모델을 평가해보자.
평균제곱편차는 , 실제값과 예측값의 차이를 제곱해서 평균하는 것이고,
평균제곱근편차는 평균제곱편차를 이 오차제곱합의 평균에 루트를 씌워주는 것이다.
평균제곱편차가 너무 큰 경우가 있으면 연산속도가 느려질 가능성이 크기 때문에 값을 작게 만들어준다.
from sklearn.metrics import mean_squared_error
from math import sqrt
sklearn 엔 복잡하게 평균제곱편차를 구하는 함수를 만들 필요가 없도록
평균제곱편차 함수가 있다.
다 불러오면 된다.
mse = mean_squared_error(dlr_test_y, prediction)
rmse = sqrt(mse)
print('score = ', dlr_model.score(X=dlr_train_X_df, y=dlr_test_y) )
print('mean_square_error (평균제곱편차) : ', mse)
print('RMSE (평균제곱근편차) : ', rmse)score = 0.5177484222203499
mean_square_error (평균제곱편차) : 2859.6963475867497
RMSE (평균제곱근편차) : 53.47612876402657값이 나왔다.
이번에는 통계적 분석을 해보자.
from statsmodels.formula.api import ols
또 최소제곱법을 사용해보자.
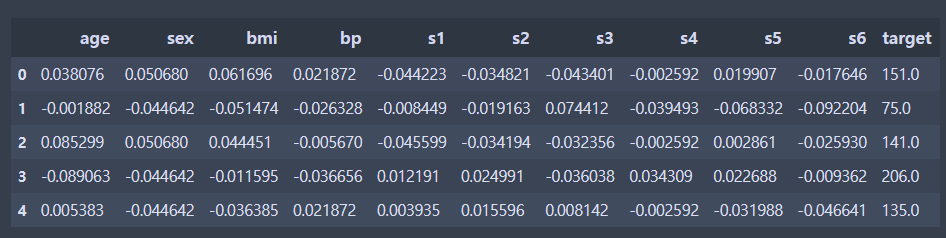
s_d_model = ols('target ~ age+sex+bmi+bp+s1+s2+s3+s4+s5+s6', df)
m_result = s_d_model.fit()
또 summary() 를 돌려보자.
m_result.summary()
다중회귀분석에서 필요한 다중공선성확인과 분산팽창요인인 VIF 를 확인해보자.
VIF 가 10을 넘으면 다중공선성이 존재하는 것이라고 했다.
from statsmodels.stats.outliers_influence import variance_inflation_factorVIF 는 다 계산해준다.
모델의 변수를 미리 알고 가야 각자의 VIF 를 알 수 있다.
# 회귀분석 모델 변수
print(s_d_model.exog_names)
['Intercept', 'age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
# age 의 VIF
print(variance_inflation_factor(s_d_model.exog, 1))VIF 를 한 번에 확인할 수 있게 데이터프레임을 만들어보자.
0번이 없고 특이하게 1번부터 age로 넘어간다.
0번은 절편이라서 그런 것 같음 .
pd.DataFrame({'컬럼' : column, 'VIF' : variance_inflation_factor(s_d_model.exog, i)}
for i, column in enumerate(s_d_model.exog_names)
if column != 'Intercept') #절편 제외
VIF 가 꽤나 많이 높은 친구들이 보인다 .
이젠 선형성을 확인해보자.
## 선형성
s_d_res_fit = m_result.predict(df)
s_d_residuals = df['target'] - s_d_res_fit# 선형성 시각화(red : 잔차)
sns.regplot(s_d_res_fit, s_d_residuals, lowess=True, line_kws= {'color' : 'red'})
plt.plot([s_d_res_fit.min(), s_d_res_fit.max()], [0, 0], '--', color='green')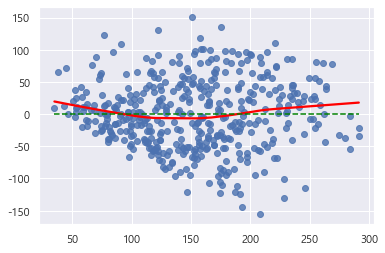
## 정규성 확인 (QQplot, 점 값이 선을 따라배치되는 것이 이상적)
s_d_sr = stats.zscore(s_d_residuals)
(s_d_x, s_d_y), _ = stats.probplot(s_d_sr)
# 정규성 시각화
sns.scatterplot(s_d_x, s_d_y)
plt.plot([-3, 3], [-3, 3], '--', color = 'grey')
정규성이 있다.
'Data Science > DATA' 카테고리의 다른 글
| [Python/statistics] 분산분석(ANOVA) - 일원분산분석(One-way ANOVA) (2) | 2022.07.30 |
|---|---|
| [Python/Data] 탐색적 데이터 분석(EDA) - 다변량 데이터 분석 (2) | 2022.07.24 |
| [Python/Data] Load_diabetes 데이터셋을 이용한 회귀분석 실습 - 단순선형회귀분석 (Simple Regression Analysis) (2) | 2022.07.21 |
| [Python/Data] 회귀분석 (Regression Analysis) 설명 (2) | 2022.07.20 |
| [Python/Data] 탐색적 데이터 분석 - 표본추출(단순확률표본추출, 계통표본추출, 층화표본추출) (1) | 2022.07.20 |




