| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Kaggle
- 2023공빅데
- 텍스트마이닝
- datascience
- machinelearning
- decisiontree
- 공빅데
- ML
- 머신러닝
- 빅데이터
- 데이터전처리
- 오버샘플링
- NLP
- 분석변수처리
- 클러스터링
- textmining
- SQL
- 데이터분석
- ADSP
- 공공빅데이터청년인턴
- 2023공공빅데이터청년인재양성
- Keras
- data
- DeepLearning
- ADsP3과목
- DL
- 2023공공빅데이터청년인재양성후기
- 공공빅데이터청년인재양성
- 공빅
- k-means
- Today
- Total
愛林
[Python/statistics] 분산분석(ANOVA) - 일원분산분석(One-way ANOVA) 본문

통계 분석에는 많은 분석법이 있다.
오늘은 종속관계에 대한 분석인 분산분석(ANOVA) 에 대해 알아보자.
분산분석 (ANOVA ; Analysis Of Variance)
분산분석(ANOVA) 는 차이의 비율이다. (F분포 사용)
모집단이 3개 이상이면서 독립변인에 의한 종속변인의 평균치 간 차이를 검정한다.
요인별 효과를 분석하거나, 3개 이상 집단 간 모평균의 차이를 분석하는데 사용한다.
Ex:) 성별, 혈액형이 다른 집단 간 키,몸무게,심박수의 차이에 유의성이 있는 지 검정.
분산분석(ANOVA) 의 검정방법은 F-test 이다. (F검정 사용)
실험집단 간 분산에 대한 실험집단 내 분산의 비율을 F통계량이라고 한다.
F통계량과 분산분석(ANOVA)
실험 집단 간 분산에 대한 실험집단 내 분산의 비율을 F통계량이라고 한다.
F 통계량 = (MSA: 집단 간 분산) / (MSE : 집단 내 분산)

관측치 = 전체 평균 + 집단 j의 처리효과 + 오차
i : 특정한 집단에 속한 관측치를 지정하는 첨자,
j : 특정한 집단을 지정하는 첨자
F통계량이 1근처이면, 집단 간 차이가 없다.
1보다 크면, 집단 간 차이가 있다.

A : ANOVA 검정 결과, 그룹 간의 차이가 없다.
B : ANOVA 검정 결과 , 그룹 사이 유의한 차이가 존재한다.
분산분석(ANOVA) 의 종류

1) 일원분산분석(One-way ANOVA)
3개 이상의 범주를 갖는 하나의 독립변수에 대한 하나의 종속변수의 평균 차이를 검정한다.
Ex:) 강남,강동,강서구 간 매장위치에 따른 만족도의 분석
2) 반복측정 분산분석(Repeated Measures ANOVA)
집단에 대한 반복 측정.
시간 흐름에 따른 여러 번 해당 결과를 반복적으로 측정하기 위한 분석 비법이다.
Ex: ) 실험 전, 실험 3개월 후, 실험 6개월 후에 따른 만족도의 분석
3) 이원분산분석(Two-way ANOVA)
두 개의 독립변수와 하나의 종속변수일 때 집단 간 차이를 분석하는 방법이다.
Ex:) 온도 1000도와 2000에 따른, 시간 1시간과 2시간 차이에 따른 맛의 변화
4) 이원반복측정 분산분석(Two-way Repeated Measures ANOVA)
실험군과 대조군을 나누어 동일한 실험 단위에 대해 여러 번 측정하는 경우에 사용된다.
시간 흐름에 따라 두 개의 독립변수에 따른 종속변수 차이를 반복적으로 분석하게 된다.
Ex:) 실험군과 대조군의 시험전, 시험 후 통증의 변화
일원분산분석(One-way ANOVA) 실습
일원분산분석은, 3개 이상의 범주를 갖는 하나의 실험요인에 대한 하나의 종속변수의 평균 차이를
검정하는 분석이었다.
stats.f_oneway() 로 scipy f통계량을 구할 수 있다.
statsmodels.stats.anova() 로 stats 모델 anova 를 구할 수 있다.
■ 증명하고자 하는 가설
4개의 각기 다른 신입사원 교육훈련 기법의 효과성을 평가하고자 한다.
새로 입사한 32명의 신입사원에게 4개 교육 기관에서 다른 학습 방법을 적용 시켰다.
한 달의 훈련기간이 끝난 후 시험을 쳤는데 그 점수는 아래와 같다. 4개 교육훈련 기법 간의 차이가 있는가 ?
만약 있다면 어떻게 다른가 ?
= > 4개 이상의 대응 표본(4개의 학습방법) 을 비교해야 하므로 일원분산분석을 사용한다.
귀무가설 : 4개의 교육훈련 기법 간의 차이가 없다.
대립가설 : 4개의 교육훈련 기법 간의 차이가 있다.
필요한 라이브러리들을 가져오자.
import os
import warnings
warnings.simplefilter(action = 'ignore', category = FutureWarning)
import numpy as np
import pandas as pd
import math
from scipy import stats # Scipy 패키지
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
import os
if os.name == 'nt' : # windows OS
font_family = "Malgun Gothic"
else : #Mac OS
font_family = "AppleGothic"
# 값이 깨지는 문제 해결을 위해 파라미터값 설정
sns.set(font=font_family, rc ={"axes.unicode_minus" : False})#데이터셋
a = [66,74,82,75,73,97,87,78]
b = [72,51,59,62,74,64,78,63]
c = [61,60,57,60,81,77,70,71]
d = [63,61,76,84,58,65,69,80]
print("a 평균 : ",np.mean(a))
print("b 평균 : ",np.mean(b))
print("c 평균 : ",np.mean(c))
print("d 평균 : ",np.mean(d))a 평균 : 79.0
b 평균 : 65.375
c 평균 : 67.125
d 평균 : 69.5
box-plot 을 이용해서 이상값을 확인해주자.
plot_data = [a,b,c,d]
plt.boxplot(plot_data)
plt.xticks([1,2,3,4], ['a', 'b', 'c', 'd'])
plt.grid(True)
plt.show()
큰 이상값은 없는 것 같다.
이제 데이터프레임으로 변환해보자.
# 데이터 프레임 변환
check = ['a', 'b', 'c', 'd']
check = [check[j] for j in range(4) for i in range(8)]
data = pd.DataFrame({'점수' : a+b+c+d, '교육기관' : check})
data.head(4)
자료의 모집단 분포는 정규분포를 따른다. 는 정규성을 검정해보자.
Shapiro-wilks Normal Test 로 정규성을 검정했다.
샤피로 정규성 검정이 정규성 검정을 가장 엄격하게 한다고 한다.
from scipy.stats import shapiro
print('정규성을 검정')
normal_a = shapiro(a)
normal_b = shapiro(b)
normal_c = shapiro(c)
normal_d = shapiro(d)
print(normal_a)
print(normal_b)
print(normal_c)
print(normal_d)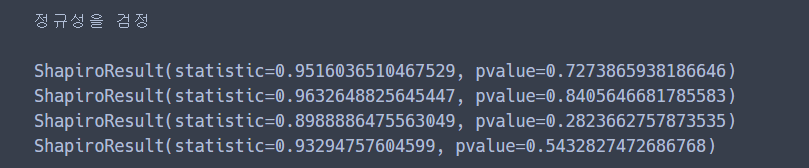
첫 번째 값은 검정 통계량이고, 두 번째 값은 p-value 이다.
정규성 검정에서는 p-value 가 유의수준 0.05 보다 큰 경우 정규성을 만족한다고 본다.
다들 0.05보다 훨씬 크므로 정규성을 만족한다고 볼 수 있다.
print(stats.ks_2samp(a,b), stats.ks_2samp(a,c), stats.ks_2samp(a,d)
, stats.ks_2samp(b,c), stats.ks_2samp(b,d), stats.ks_2samp(c,d), sep="\n")
ks_2samp 으로 집단 간의 정규성을 확인했다.
ks_2samp 는 Two-sample KS(Kolmogorow-Smirnow) 테스트이다.
이제 등분산성을 검정해보자.
등분산성은 모든 집단의 모분산은 동일하다는 것을 말한다.
ANOVA 를 진헹하기 위해서는, 두 집단의 모분산이 동일해야 한다.
## 등분산성 검정 : 모든 집단의 모분산은 동일하다
print('등분산성 검정')
# levene 등분산성 검정
from scipy.stats import levene
print(levene(a,b,c,d))
# bartlett 등분산성 검정
from scipy.stats import bartlett
print(bartlett(a,b,c,d))
Levene 등분산성 검정과 bartlett 등분산성 검정이 있다.
scipy.stats 에서 불러올 수 있다.

p-value 가 모두 0.05보다 크므로 등분산성을 만족한다.
F통계량을 이용한 ANOVA (stats.f_oneway)
이제 F통계량을 이용하여 가설을 검정해보자.
f_statistic, pval = stats.f_oneway(a,b,c,d)
print('F={0:.1f}, p={1:.3f}'.format(f_statistic, pval))
if pval < 0.05 :
print("귀무가설 기각, 4개의 교육훈련기법 간 차이가 있다.")
else :
print("귀무가설 채택, 4개의 교육훈련기법 간 차이가 없다.")stats.f_oneway 에 a,b,c,d 데이터들을 넣어주었다.
t_statistic 은 t 검정 통계량, pval 은 p-value 를 보여준다.
p-value 가 0.05보다 작으면, 기각역이므로 귀무가설은 기각되고
4개의 교육기법은 차이가 있다 라는 대립가설이 채택된다.

결과는 기각역.
p-value 가 0.029 < 0.05 이므로 대립가설이 채택되었다.
4개의 교육훈련기법 간에는 차이가 있다.
Statsmodel 을 이용한 ANOVA (statsmodel.anova)
이번에는 f통계량이 아닌, Statsmodel 을 이용하여 가설을 검정해보자.
model = ols('종속변수 ~ 독립변수' , data).fit() : model
sm.stats.anova_lm(model,type=2) 를 사용하면 Type2 아노바 데이터프레임이다.
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lmmodel_1A = ols('점수 ~ C(교육기관)', data).fit()
anova_lm_result = anova_lm(model_1A)
anova_lm_result
교육 기관 간 평균 편차는 295.0833,
Residual 은 잔차이다. 편차 이는 C 집단 내 편차를 이야기한다.
왜 이렇게 나왔느냐,
우리가 아까 만든 data 데이터프레임은

대충 이렇다.
data.shape 을 찍어보면 32, 2가 나온다,
여기서 SSA(집단간 제곱합) 는 K-1 이므로 4-1 = 3
SSE(집단내 제곱합) 는 N-K 이므로 32 - 4 = 28
SST(총 제곱합) 는 N-1 = 32 - 1 = 31
MSA(집단 간 분산) / MSE(집단 내 분산) = 295.083333 / 84.741071 = 3.482176 이다. (F통계량)
PR(>F) 는 p-value 이다. 아까 구한 0.029 와 비슷한 값인 0.028897 이 나왔다.
pval = anova_lm_result['PR(>F)'][0]
if pval < 0.05 :
print("귀무가설 기각, 4개의 교육훈련 기법간에 차이가 있다.")
else :
print("귀무가설 채택, 4개의 교육훈련 기법간에 차이가 없다.")

귀무가설 기각, 4개의 교육훈련 기법간에 차이가 있다.
사후분석
F검정을 통해서 집단 간 차이가 유의하더라도, 어떤 집단 간의 차이인지 명확하게 확인하기 위해서
사후검정(Post-hoc Analysis) 을 진행한다. (유의미하지 않을 시에는 사후 분석이 불필요하다.)
사후 검정 방식 중에 대표적인 것은 Tukey, Bonferonni, Scheff 이다.
사후 검정 민감도는 Scheffe > Tukey > Duncan 순이다.

위에서 구한 결과로 사후 분석을 진행해보자,
ANOVA 검증 결과 유의미하다는 결론을 얻었을 때, 구체적으로 어떤 수준에서 평균 차이가 나는 지를
검증해야 할 필요가 있다.
Tukey 의 HSD 를 사용해서 사후 분석을 진행해볼 것이다.
from statsmodels.stats.multicomp import pairwise_tukeyhsd
HSD = pairwise_tukeyhsd(data['점수'], data['교육기관'], alpha = 0.05)
HSD.summary()
Tukey 의 HSD 를 이용하여 사후 분석을 실시한 결과,
a조건과 b조건에서 유의미한 평균 차이가 있었다. (True) (p<0.05)
이원분산분석 (Two-way ANOVA)
이원분산분석은 종속변수가 1개, 독립변수가 2개이면서 독립변수 각각이 요인으로서 요인 내에
수준을 가지고 있을 때, 각 집단 평균의 유의미한 차이가 있는 지 유무를 확인한다.
■ 증명하고자 하는 가설
귀무가설 : 강도에 대한 각 판유리와 온도 간에는 상호작용 효과가 없다.
대립가설 : 강도에 대한 각 판유리와 온도 간에는 상호작용 효과가 있다.
dat=pd.DataFrame({'판유리':['유리1', '유리1', '유리1', '유리2', '유리2', '유리2', '유리3', '유리3',
'유리3', '유리1', '유리1', '유리1', '유리2', '유리2', '유리2', '유리3',
'유리3', '유리3', '유리1', '유리1', '유리1', '유리2', '유리2', '유리2',
'유리3', '유리3', '유리3'],
'온도':[100, 100, 100, 100, 100, 100, 100, 100, 100, 125, 125, 125, 125, 125,
125, 125, 125, 125, 150, 150, 150, 150, 150, 150, 150, 150, 150],
'강도':[580, 568, 570, 550, 530, 579, 546, 575, 599, 1090, 1087, 1085, 1070,
1035, 1000, 1045, 1053, 1066, 1392, 1380, 1386, 1328, 1312, 1299, 867,
904, 889]
})
dat 데이터를 만들어주었다.

우리의 종속변수는 '강도' 이고,
독립변수는 '판유리' 와 '온도' 이다.
판유리와 온도 요인으로 구분한 각 집단별 표본 수는 모두 3으로 동일했다.
dat.groupby(['판유리', '온도']).agg(len)
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
model = ols('강도 ~ C(판유리) * C(온도)', dat).fit()
anova_result = pd.DataFrame(anova_lm(model))위에서 했던 거 똑같이 해준다.
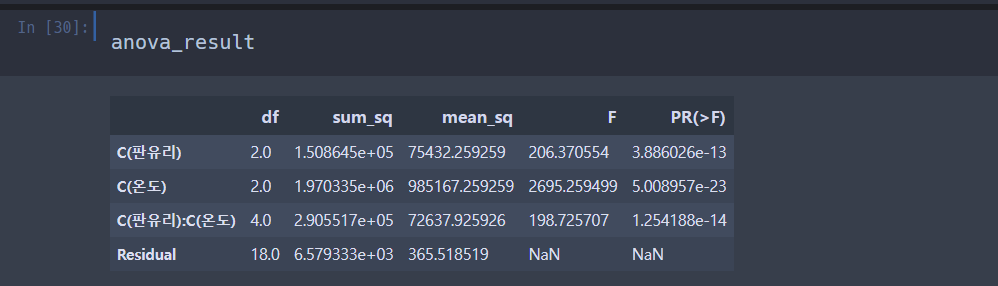
판유리 : F(2,18) = 206.370554 . p-value < 0.05 로 유의미하다. 즉 판유리의 수준에 따라 평균에 차이가 난다.
온도 : F(2,18) = 2695.259499 , p-value < 0.05 로 유의미하다. 즉, 온도에 따라 평균에 차이가 난다.
판유리와 온도 F(4,18) = 198.725707, p-value < 0.05 로 유의미하다. 상호작용 효과를 발견했다.
이제 사후분석을 진행해보자. Tukey 의 HSD 사용.
dat['온도'] = dat['온도'].astype('str')
dat['combi'] = dat.판유리 + "/" + dat.온도
print(pairwise_tukeyhsd(dat['강도'], dat['combi'])) Multiple Comparison of Means - Tukey HSD, FWER=0.05
===========================================================
group1 group2 meandiff p-adj lower upper reject
-----------------------------------------------------------
유리1/100 유리1/125 514.6667 0.0 459.9706 569.3627 True
유리1/100 유리1/150 813.3333 0.0 758.6373 868.0294 True
유리1/100 유리2/100 -19.6667 0.9307 -74.3627 35.0294 False
유리1/100 유리2/125 462.3333 0.0 407.6373 517.0294 True
유리1/100 유리2/150 740.3333 0.0 685.6373 795.0294 True
유리1/100 유리3/100 0.6667 1.0 -54.0294 55.3627 False
유리1/100 유리3/125 482.0 0.0 427.3039 536.6961 True
유리1/100 유리3/150 314.0 0.0 259.3039 368.6961 True
유리1/125 유리1/150 298.6667 0.0 243.9706 353.3627 True
유리1/125 유리2/100 -534.3333 0.0 -589.0294 -479.6373 True
유리1/125 유리2/125 -52.3333 0.067 -107.0294 2.3627 False
유리1/125 유리2/150 225.6667 0.0 170.9706 280.3627 True
유리1/125 유리3/100 -514.0 0.0 -568.6961 -459.3039 True
유리1/125 유리3/125 -32.6667 0.5066 -87.3627 22.0294 False
유리1/125 유리3/150 -200.6667 0.0 -255.3627 -145.9706 True
유리1/150 유리2/100 -833.0 0.0 -887.6961 -778.3039 True
유리1/150 유리2/125 -351.0 0.0 -405.6961 -296.3039 True
유리1/150 유리2/150 -73.0 0.0046 -127.6961 -18.3039 True
유리1/150 유리3/100 -812.6667 0.0 -867.3627 -757.9706 True
유리1/150 유리3/125 -331.3333 0.0 -386.0294 -276.6373 True
유리1/150 유리3/150 -499.3333 0.0 -554.0294 -444.6373 True
유리2/100 유리2/125 482.0 0.0 427.3039 536.6961 True
유리2/100 유리2/150 760.0 0.0 705.3039 814.6961 True
유리2/100 유리3/100 20.3333 0.918 -34.3627 75.0294 False
유리2/100 유리3/125 501.6667 0.0 446.9706 556.3627 True
유리2/100 유리3/150 333.6667 0.0 278.9706 388.3627 True
유리2/125 유리2/150 278.0 0.0 223.3039 332.6961 True
유리2/125 유리3/100 -461.6667 0.0 -516.3627 -406.9706 True
유리2/125 유리3/125 19.6667 0.9307 -35.0294 74.3627 False
유리2/125 유리3/150 -148.3333 0.0 -203.0294 -93.6373 True
유리2/150 유리3/100 -739.6667 0.0 -794.3627 -684.9706 True
유리2/150 유리3/125 -258.3333 0.0 -313.0294 -203.6373 True
유리2/150 유리3/150 -426.3333 0.0 -481.0294 -371.6373 True
유리3/100 유리3/125 481.3333 0.0 426.6373 536.0294 True
유리3/100 유리3/150 313.3333 0.0 258.6373 368.0294 True
유리3/125 유리3/150 -168.0 0.0 -222.6961 -113.3039 True
-----------------------------------------------------------
해석 : 유리 1도가 100도일 때와 125도일 때의 유의미한 차이가 있었고,
100도와 150도일 때에도 유의미한 차이가 있었다.
그렇지만 유리 1과 유리 2가 100도일 때는 유의미한 차이가 없었다.
.
.
.
.

ANOVA 는 더 공부해야겠다 ..
뭔가 복잡한 기분.. 어려웡 ㅠ
※ 해당 자료는 모두 공공 빅데이터 청년 인턴 교육자료들을 참고합니다.




