| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- data
- ML
- 분석변수처리
- Keras
- DL
- 오버샘플링
- 공빅데
- 텍스트마이닝
- 2023공공빅데이터청년인재양성후기
- 공공빅데이터청년인재양성
- datascience
- 데이터전처리
- ADsP3과목
- 머신러닝
- 데이터분석
- SQL
- 클러스터링
- 2023공공빅데이터청년인재양성
- 공빅
- k-means
- decisiontree
- DeepLearning
- textmining
- NLP
- 빅데이터
- Kaggle
- machinelearning
- 2023공빅데
- ADSP
- 공공빅데이터청년인턴
- Today
- Total
愛林
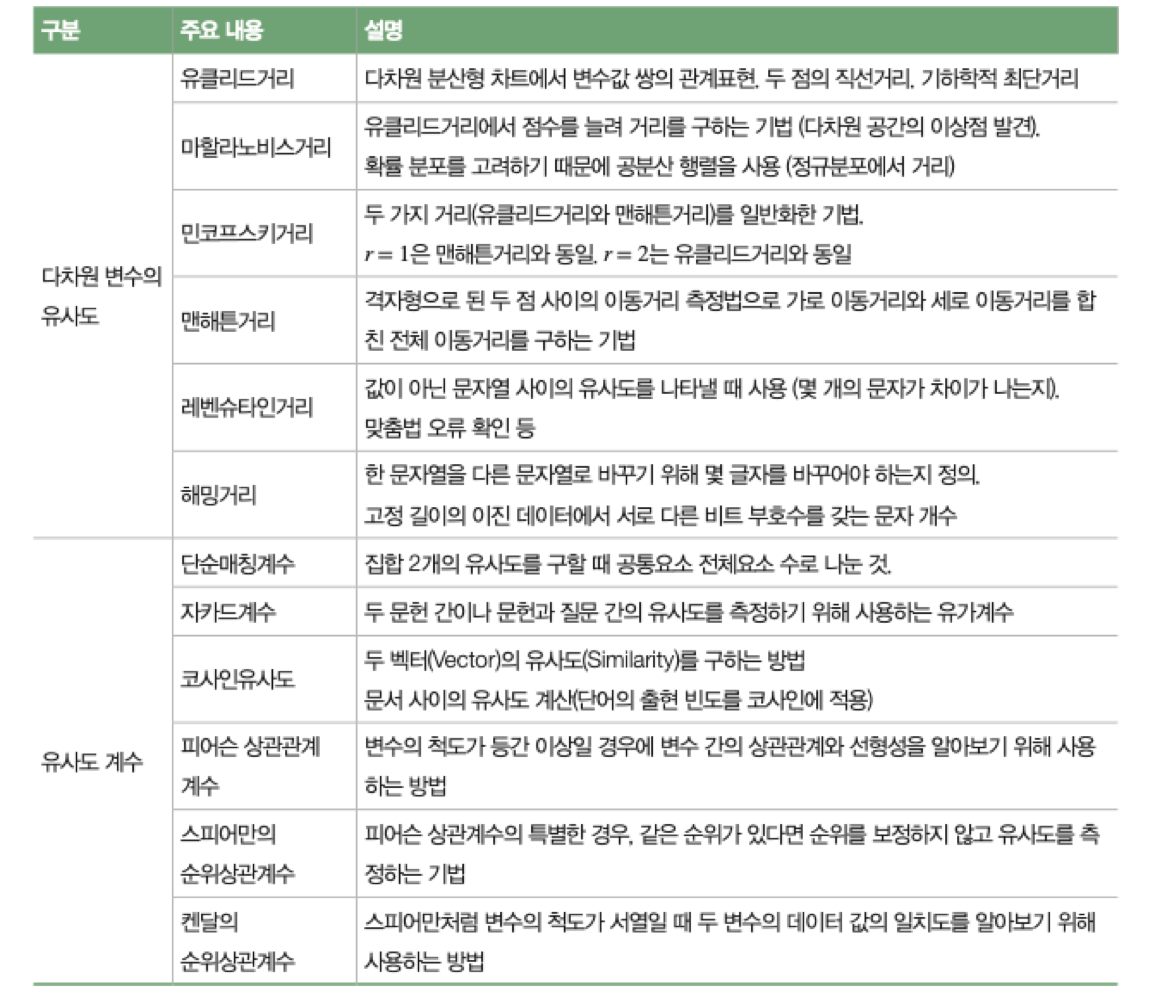
데이터의 유사도(Similarity) 와 비유사도(Dis-Similarity, = 거리(Distance)) 본문
데이터의 유사도(Similarity) 와 비유사도(Dis-Similarity, = 거리(Distance))
愛林 2022. 8. 6. 00:44
K-NN 이나 우리가 이 다음에 알아볼 다른 머신러닝 기법들을 배우기 이전에,
먼저 데이터의 유사도와 비유사도 그리고 이를 측정하는 척도를 알아가는 것은
중요하다.
또한 군집분석을 할 때도 사용했었던 것들이다.
먼저 알아보도록 하자.
데이터 유사도, 비유사도
비유사도 ( Dis - Similarity , 거리(Distance) )
두 개체(Object) 의 다른 정도에 대한 수치적인 척도로, 두 개체의 쌍이 더 닮을 수록 낮아진다.
Distance(거리) 는 비유사도의 동의어이다.
하한은 0, 상한은 제한이 없다.
0에 가까우면 유사한 것 (거리가 가까운 것),
1에 가까우면 유사한 것이 아닌 것 (거리가 먼 것) 이다.
유사도 ( Similarity )
두 개체(Object) 의 닮은 정도에 대한 수치적인 척도이다.
음이 아닌 수, 0과 1 사이의 값으로 보통 표현한다.
1에 가까우면 유사, 0에 가까우면 유사하지 않다.
피어슨 상관계수와 유사하며, 값이 1이나 -1에 가까울수록 관계가 있고 유사하다는 것을 생각하면 된다.
유사도를 비유사도로 변환하거나 그 역으로 변환해서 근접도 척도를 [0,1] 과 같은 특정 범위로
적용하기 위해 사용하는 것을 변환 이라고 한다.
데이터 유사도와 비유사도의 측정 = 거리 (Distance)
개체 간의 비유사도 (거리)의 측도는 데이터와 데이터간의 유사성을 보는 군집분석 뿐만 아니라
변수와 변수 간 관계를 보는 다변량 통계 분석에서도 사용된다.

여기서 가장 많이 쓰이는 거리는 맨해튼 거리(Manhattawn Distance),
유클리드 거리 (Euclidean Distance) 이다.
맨해튼 거리는 거리를 가로블록과 세로 블록 절대합으로 계산되는 방식에서
착안한 거리척도이다.
r = 1 거리는 맨해튼거리를 말한다.

유클리드 거리는 두 점을 잇는 가장 짧은 직선거리를 측정하는 척도이다.
r = 2 거리는 유클리드 거리를 말한다.

이외에도 다양한 거리 척도들이 있다.
실습
X = [[5,4,3],[1,7,9]]
X를 먼저 정의해주고 ,
from sklearn.neighbors import DistanceMetric
sklearn 의 DistanceMetric 을 불러온다.
DistanceMetric 은 안에 우리가 위에서 배웠던 거리들이 들어있는 클래스이다.
DistanceMetric.get_metric('거리이름') 으로 사용한다.
유클리드 거리
dist_euclidean = DistanceMetric.get_metric('euclidean')
print(dist_euclidean.pairwise(X))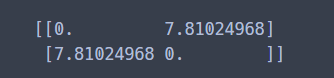
맨해튼 거리
dist_manhattan = DistanceMetric.get_metric('manhattan')
print(dist_manhattan.pairwise(X))
해밍 거리
한 문자열을 다른 문자열로 바꾸기 위해 몇 글자를 바꾸어야 하는 지를 정의한다.
고정 길이의 이진 데이터에서 서로 다른 비트 부호수를 갖는 문자 개수를 찾는다.
dist_hamming = DistanceMetric.get_metric('hamming')
print(dist_hamming.pairwise(X))
X = [[5,4,3],[1,7,9]]
이었으므로 , 안에있는 요소들이 다 다르므로 다 바꾸어주어야 한다
그러므로 1이 나옴. (100% 다 바꿔야한다는 뜻이다.)

그렇다면 한 개만 중복되는 것이 있는 경우에는 ?
Y 를 정의해보고 , Haming 거리에 넣어보자.
Y = [[1,4,3],[1,7,9]]
print(dist_hamming.pairwise(Y))
3개 중에서 2개만 바꾸면 되니까 0.67 % 정도 바꾸면 되므로, 0.67이 나왔다.
Haming 거리는 정확하게 같은 지에 대한 여부만 고려한다.
이 여부에서 다른 값을 count 하는 것이다.
민코우스키거리
두 가지 거리 (맨해튼거리, 유클리드 거리) 를 일반화한 거리이다.
p=1 은 맨해튼거리, p=2 는 유클리드 거리이다.
dist_minkowski = DistanceMetric.get_metric('minkowski', p=2) # 유클리드 거리
print(dist_minkowski.pairwise(X))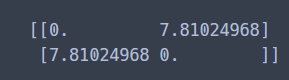
p = 2 는 유클리드 거리였으므로, 위에서 유클리드 거리를 실습했던 것과
같은 수가 나왔다.
dist_minkowski = DistanceMetric.get_metric('minkowski', p=1) # 맨해튼 거리
print(dist_minkowski.pairwise(X))
p = 1 은 맨해튼 거리였으므로, 위에서 맨해튼 거리를 실습했던 것과
같은 수가 나왔다.
※ 해당 자료는 모두 공공 빅데이터 청년 인턴 교육자료들을 참고합니다.
'Data Science > Machine Learning' 카테고리의 다른 글
| [Python/MachineLearning] Boston Housing Price Data 를 이용한 Decision Tree 실습 (2) | 2022.08.15 |
|---|---|
| [Python/MachineLearning] Decision Tree(의사결정나무) (2) | 2022.08.15 |
| [Python/ML] K-NN (K-Nearest Neigthbor , K-최근접이웃) (1) | 2022.08.06 |
| [Python/Machine Learning] ML-Clustering (군집분석) : K-Means (4) | 2022.07.30 |
| 분류 알고리즘 (Classification Algorithm), 분류 알고리즘의 종류 (2) | 2022.07.27 |




