| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- datascience
- 클러스터링
- 2023공빅데
- ADSP
- Kaggle
- data
- 2023공공빅데이터청년인재양성후기
- 분석변수처리
- 머신러닝
- textmining
- 텍스트마이닝
- 공공빅데이터청년인턴
- DL
- 공빅
- 공공빅데이터청년인재양성
- decisiontree
- ML
- 공빅데
- ADsP3과목
- 데이터전처리
- 데이터분석
- DeepLearning
- NLP
- 2023공공빅데이터청년인재양성
- machinelearning
- 오버샘플링
- Keras
- SQL
- k-means
- 빅데이터
- Today
- Total
愛林
[Python/ML] K-NN (K-Nearest Neigthbor , K-최근접이웃) 본문
이전에도 배웠던 적이 있는 K-NN 기법에 대해서 자세히 알아보도록 하자.
K-NN (K-Nearest Neightbor)
입력과 결과가 있는 데이터들이 주어진 상황에서 , 새로운 입력에 대한 결과를 추정할 때,
결과를 아는 최근접한 k개의 데이터에 대한 결과 정보를 이용하는 방법이다.
데이터 간의 거리를 계산해서, 효율적으로 근접한 이웃을 탐색 후
이 탐색한 근접 이웃 k 개로부터 결과를 추정하게 된다.
분류(Classification) 알고리즘에 속한다.4
여기서 사용되는 데이터 간의 거리는, 유클리디언 거리(Euclidian Distance) 이다.
즉, 직선 거리를 사용한다.
최근접 k개로부터 결과를 추정하는 방법은,
분류와 예측(회귀) 가 있는데, 차이는 이와 같다.
| 구분 | 분류 | 예측(회귀) |
| 목적 | 유사한 레코드들 중에 다수가 속한 클래스가 무엇인지 찾은 후 새로운 레코드를 그 클래스로 분류 | 유사한 레코드들의 평균을 찾아서 새로운 레코드들에대한 예측값으로 사용 |
| 특징 | 출력이 범주형 값 다수결 투표( majority voting) : 개수가 많은 범주를 선택한다. |
출력이 수치형 값이다. 평균 : 최근접 k 개의 평균값, 가중치 합 : 거리에반비례하는 가중치 사용 |

예를 들어, 위의 그림에서 K 가 3일 때,
가장 가까운 3개의 데이터 클래스를 다수결에 따라서 새로운 데이터의 클래스로 분류한다.
겉에 빨간 테두리가 있는 원은 새로운 데이터(New Data) 이다.
왼쪽 위의 회색 점 New Data 는 주변 3개의 범주가 회색이기에, 새로운 데이터로 회색으로 분류된다.
중간에 있는 회색 점 New Data 는 주변의 2개가 회색이고 1개가 파란색이기에,
새로운 데이터는 회색으로 분류된다.
맨 오른쪽의 파란 점 New Data 는 주변의 2개가 파란색이고, 1개가 회색이기에
새로운 데이터는 파란색으로 분류된다.
Breast Cancer Data 를 이용한 K - NN 실습
먼저 , KNN 실습을 할 때 필요한 라이브러리들을 불러오자.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier ## K-NN
from sklearn.metrics import confusion_matrix, classification_report
우리가 오늘 실습 때 사용할 데이터는 sklearn 에서 제공하는 데이터셋인
유방암 데이터 (Breast cancer Data) 를 사용할 것이다.
불러오자.
## 데이터셋
from sklearn.datasets import load_breast_cancer
# 데이터 불러오기
data = load_breast_cancer()
# 독립변수 (inpurt data)
b_input_data = data['data']
# 종양 : 악성(0), 양성(1) 여부 (target data)
b_target_data = data['target']
# 종양 구분
tumar = data['target_names']
load_breast_cancer를 불러와서 data 에 저장해주었다,
독립변수 (X) 는 data를 b_input_data 로 저장해 주었고,
종양의 여부 (Target Data) 를 b_target_data 에 넣어주었다.
악성은 0, 양성은 1이다.
data 의 target_names 데이터 (종양 구분 데이터) 는 tumar 에 넣어주었다.
# 속성 명칭
feature_names = data['feature_names']
print('종양 여부 결정 속성 : {}'.format(feature_names))
print('종양 구분 : {}'.format(tumar))
breast_df = pd.DataFrame(b_input_data, columns = feature_names)
breast_df['target'] = b_target_data
feature names 속성의 이름들은 feature_names 에 저장해주었다.
이 데이터들은 종양의 여부를 결정하는 속성들이다.
한번 확인해보면..
종양 여부 결정 속성 : ['mean radius' 'mean texture' 'mean perimeter' 'mean area'
'mean smoothness' 'mean compactness' 'mean concavity'
'mean concave points' 'mean symmetry' 'mean fractal dimension'
'radius error' 'texture error' 'perimeter error' 'area error'
'smoothness error' 'compactness error' 'concavity error'
'concave points error' 'symmetry error' 'fractal dimension error'
'worst radius' 'worst texture' 'worst perimeter' 'worst area'
'worst smoothness' 'worst compactness' 'worst concavity'
'worst concave points' 'worst symmetry' 'worst fractal dimension']
종양 구분 : ['malignant' 'benign']약 30개의 속성과 malignant(악성), benign(양성) 이 들어있다.
속성명에 공백이 들어있으니 이 공백을 이렇게_"_"를_넣어서_빈_자리를_채워주자
breast_df.columns = [col.replace(" ", "_") for col in breast_df.columns]
양성과 악성의 비율을 확인해보자.
breast_df['target'].value_counts()1 357
0 212
Name: target, dtype: int64
이제 본격적으로 K-NN 을 실습하기 위한
학습 데이터셋을 만들어주자.
## 학습 데이터셋 생성
# 평균 관련된 3개의 속성으로 종양 여부 판단
model_feature_name = ['mean_radius', 'mean_texture', 'mean_perimeter']
X = breast_df[model_feature_name]
Y = breast_df['target']
평균과 관련된 3개의 속성으로 종양 여부를 판단할 것이다.
mean_radius, mean_textrue, mean_perimeter 를 사용한다.
X 독립변수 데이터에 평균과 관련된 3개의 데이터를 넣어주고,
Y 는 종양의 악성, 양성 데이터 (Target 데이터) 를 넣어준다.
# 80% 데이터를 학습 데이터로, 20% 를 테스트 데이터로.
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.2, random_state= 20)80% 의 데이터를 학습 데이터로, 나머지 20%는 테스트 데이터로 사용한다.
random_state 는 20 으로 해서 난수 생성을 맞추어 준다.
거리 기반 알고리즘들은 기본적으로 표준화와 정규화의 수행이 필요하다.
StandardScaler 를 사용해서 표준화시켜주었다.
from sklearn.preprocessing import StandardScaler
## 스케일링 & 정규화
scaler = StandardScaler()
X_train_std = scaler.fit_transform(X_train)
X_test_std = scaler.fit_transform(X_test)
각 3개 속성의 표준화시킨 결과를 확인해보자.
# 스케일링 (각 속성 3개에 대한 표준화 수행 결과 확인)
for col in range(3) :
print(f'평균 = {X_train_std[:,col].mean()}, 표준편차 {X_train_std[:,col].std()}')
for col in range(3) :
print(f'평균 = {X_test_std[:,col].mean()}, 표준편차 = {X_test_std[:,col].std()}')평균 = -6.109886711343719e-16, 표준편차 1.0000000000000002
평균 = -3.2833320921661774e-15, 표준편차 1.0000000000000002
평균 = 2.851931145454688e-15, 표준편차 1.0000000000000004
평균 = -1.1472304587793285e-15, 표준편차 = 1.0
평균 = 4.4798472923471226e-17, 표준편차 = 0.9999999999999999
평균 = -1.1842378929335002e-15, 표준편차 = 0.9999999999999998평균도 0에 가깝고, 표준편차도 1로 잘 맞추어진 것 같다.
정규화가 잘 이루어졌다.
이제 K-NN 분류기를 생성해보자.
가장 가까운 3개 중에서 1개가 A , 2 개가 C이면 C로 분류가 된다.
knn_clf = KNeighborsClassifier(n_neighbors = 3)
KNN 분류기를 knn_clf 로 저장해주었다.
# 분류기 학습
knn_clf.fit(X_train_std, y_train)
# 예측
y_pred = knn_clf.predict(X_test_std)
x_train_std 데이터와 y_train 데이터를 넣어주어서 학습시켰다.
y_pred 에 predict 한 데이터를 넣어준다.
이제 이 테스터셋의 정확도를 확인해보자.
## 모델 평가
print("테스트 세트 정확도 : {:.2f}".format(knn_clf.score(X_test_std, Y_test)))테스트 세트 정확도 : 0.91
0.96이면 꽤나 높다.
혼동행렬로 확인해보자.

conf_Matrix = confusion_matrix(y_test, y_pred)
print(conf_Matrix)
크로스로 보았을 때 맞게 된 것이 42, 62이므로 잘 된 것 같다.
report = classification_report(y_test, y_pred)
print(report)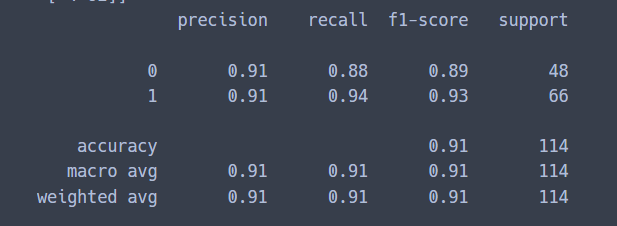
정밀도 0.91,
재현율 0.88, 0.94
잘 나온 것 같다.
그렇지만, 0.91 은 조금 부족한 것 같으니 모델을 좀 더 개선시켜 보자.
k값을 변화시킬 때, accuracy 가 증가하는 지 확인한다.
accuracy_knn = []
for i in range(1,31) :
knn = KNeighborsClassifier(n_neighbors = i)
knn.fit(X_train_std, y_train)
pred_i = knn.predict(X_test_std)
accuracy_knn.append(knn.score(X_test_std, y_test))
print(accuracy_knn)
k 를 1부터 30까지 변화시켜서 확인한다.
[0.8859649122807017, 0.8771929824561403, 0.9122807017543859, 0.9122807017543859,
0.956140350877193, 0.9298245614035088, 0.9385964912280702, 0.9385964912280702,
0.9385964912280702, 0.9210526315789473, 0.9385964912280702, 0.9210526315789473,
0.9385964912280702, 0.9298245614035088, 0.9298245614035088, 0.9298245614035088,
0.9298245614035088, 0.9298245614035088, 0.9298245614035088, 0.9298245614035088,
0.9298245614035088, 0.9298245614035088, 0.9385964912280702, 0.9298245614035088,
0.9385964912280702, 0.9210526315789473, 0.9210526315789473, 0.9210526315789473,
0.9385964912280702, 0.9385964912280702]음 확실히 이렇게 보니 잘 모르겠다.
시각화 시켜서 확인해보자.
plt.plot(range(1,31), accuracy_knn, marker = 'o')
plt.title("Accuracy with K-value")
plt.xlabel('k-label')
plt.ylabel('Accuracy')
plt.show()
k 가 5일 때 정확도가 가장 높은 것 같다.한 0.96정도
k = 5 로 해서 knn 을 돌려보자.
## Accuracy 결과로 학습 / 예측 (Training/Prediction)
knn_clf = KNeighborsClassifier(n_neighbors = 5)
# 분류기 학습
knn_clf.fit(X_train_std, y_train)
# 예측
y_pred = knn_clf.predict(X_test_std)
print("예측결과:\n", y_pred[:10])
# test_set
print("정답 : \n", list(y_test)[:10])예측결과:
[1 0 0 1 0 0 0 1 1 0]
정답 :
[1, 0, 0, 1, 0, 0, 0, 1, 1, 0]
오 예측한 값 10개와 정답인 값 10개를 비교해보니,
똑같이 나왔다.
그렇다면 이제 점검을 해보자.
print("테스트 세트 정확도 : {:.2f}".format(knn_clf.score(X_test_std, y_test)))테스트 세트 정확도 : 0.96
아까 전엔 정확도가 0.91 이었는데 이젠 0.96이다.
개선됐다.
혼동행렬을 확인해보자.
conf_matrix = confusion_matrix(y_test, y_pred)
print(conf_matrix)[[44 4]
[ 1 65]]아까보다 조금 더 개선된 결과가 보인다.

classification_report 을 사용한 결과도 확인해보자.
report = classification_report(y_test, y_pred)
print(report)
이번에도 아까보다 조금 더 개선된 결과가 보인다.

신기한 머신러닝의 세계 ..
'Data Science > Machine Learning' 카테고리의 다른 글
| [Python/MachineLearning] Boston Housing Price Data 를 이용한 Decision Tree 실습 (2) | 2022.08.15 |
|---|---|
| [Python/MachineLearning] Decision Tree(의사결정나무) (2) | 2022.08.15 |
| 데이터의 유사도(Similarity) 와 비유사도(Dis-Similarity, = 거리(Distance)) (1) | 2022.08.06 |
| [Python/Machine Learning] ML-Clustering (군집분석) : K-Means (4) | 2022.07.30 |
| 분류 알고리즘 (Classification Algorithm), 분류 알고리즘의 종류 (2) | 2022.07.27 |




